高校の数学から理解する量子コンピュータ（１）

量子コンピュータを理解するには、数学が必要なのは言うまでありません。とくに複素数、ベクトル、行列などの知識が重要です。ここでは、これらと量子力学との関係をみてみることにします。

複素数と三角関数

複素数とは

「数」には、自然数、整数、有理数、無理数、虚数といろいろなものがあります。

自然数
１，２，３・・・物を、１個、２個、３個と数えます。

整数
自然数に、０や負の数をくわえた数です。

有理数
つまり、$1/3$ などの分数です。

無理数
整数の分数では、表せない数。例えば、円周率 $\pi=3.1415 \cdots$、２の平方根 $\sqrt{2}=1.4142\cdots$ などです。

実数
有理数と無理数の総称です。

虚数
負の数字の平方根。二乗すると－１になるような数。虚数単位 $i=\sqrt{-1}$ に実数をかけて表せます。

複素数
２つの実数、$a$, $b$ と、虚数単位 $i$ を用いて、$a+bi$ と表せる数です。

波を表すのに便利な複素数

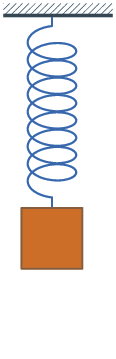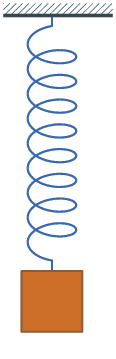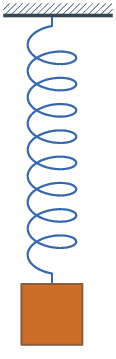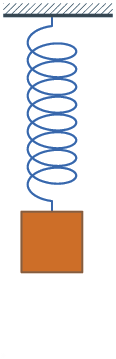
例えば、バネによって吊り下げられた重りの振動は、平衡点まわりでは正弦波（サインカーブ）、または余弦波（コサインカーブ）で表わせます。

余弦波で表すと、$\omega$ を角周波数、位相を$\phi$ として、時間 $t$ にたいして、次のように記述できます。

$$A \cos (\omega t+\phi)$$
これを、複素数をもちいて表すと、次のようになります。実部が、実際の波に相当します。
$$A[\cos (\omega t+\phi)+i \sin (\omega t+\phi)]=A e^{i \phi} e^{i \omega t}$$
ここで、オイラーの公式 $e^{j \theta}=\cos \theta+j \sin \theta$ が使われています。
時間 $\tau$ だけ進んだ状態は、複素数を掛け算することによって得られます。
$$
A e^{i \phi} e^{i \omega t} \times e^{i \omega \tau}=A e^{i \phi} e^{i(\omega t+\tau)}
$$
量子力学では、粒子の振る舞いは、波動方程式（シュレディンガー方程式）に従う波として扱われ、空間の点 $x$ にあるのは波としての複素数ということになります。それは波動関数と呼ばれ、$\psi(x)$ と書かれます。波動関数の値は、確率振幅と呼ばれ、この複素数の絶対値の２乗が、その粒子が位置 $x$ に存在する確率ということになります。

ここで、ちょっと寄り道をして、バネ振子や連成振動振動をみてみます。

バネでつるされた重りの振動（バネ振り子）

上の図のバネ振子の振動を、古典力学的に解いてみましょう。

重りがバネの力とつり合あったの位置を原点 0 として、 $x$ 軸を考え，時刻 $t$ での重りの位置を $x(t)$ とします。

重りに作用する力 $F$ は，ばねの力で決まります。つり合いの位置を、0 にしているので、重力の影響を考慮する必要はありません。
$$ F = -kx$$
力 $F$ を受けて運動する質量 $m$ の重りの運動方程式は次のようになります。
$$m \frac{d^{2} x}{d t^{2}}=-k x$$
$\omega=\sqrt{\frac{k}{m}}$ とすると、運動方程式は、次のようになります。

$$\frac{d^{2} x}{d t^{2}}+\omega^{2} x=0$$
この微分方程式の解は、以下のようになります。

$$
x(t)=A \cos (\omega t+\alpha) \quad(A, \alpha: \text { 任意定数 })
$$

微分方程式の解き方

解を、$x=e^{\lambda t}$ とおくと、
$$\frac{d^{2} x}{d t^{2}}+\omega^{2} x=\lambda^{2} e^{\lambda t}+\omega^{2} e^{\lambda t}=\left(\lambda^{2}+\omega^{2}\right) e^{\lambda t}=0$$
となり、特性方程式 $\lambda^{2}+\omega^{2}=0$ が得られ、その解は、$\lambda=\pm i \omega$ となります。$\lambda_{1}=i \omega, \quad \lambda_{2}=-i \omega$ とすると、運動方程式の解は、独立な解$e^{\lambda_{1} t}, \quad e^{\lambda_{2} t}$ の線形結合として求まります。
$$
\left.x=c_{1} e^{\lambda_{1} t}+c_{2} e^{\lambda_{2} t}=c_{1} e^{i \omega t}+c_{2} e^{-i \omega t} \quad\left(c_{1}, c_{2}: \text { 任意定数（複素数 }\right)\right)
$$
オイラーの公式 $e^{\pm i \theta}=\cos \theta \pm i \sin \theta$ を用いると、
$x=c_{1}(\cos \omega t+i \sin \omega t)+c_{2}(\cos \omega t-i \sin \omega t)=\left(c_{1}+c_{2}\right) \cos \omega t+i\left(c_{1}-c_{2}\right) \sin \omega t$
と書けます。物理量 $x$ が実数であることを考えると、$c_{1}=\left(A_{1}+i A_{2}\right) / 2, \quad c_{2}=\left(A_{1}-i A_{2}\right) / 2$ とおいて、
$$
x=A_{1} \cos \omega t+A_{2} \sin \omega t \quad\left(A_{1}, A_{2}: \text { 任意定数 (実数 }\right) \text { ) }
$$
が求まります。

$A=\sqrt{A_{1}^{2}+A_{2}^{2}}, \quad \cos \alpha=A_{1} / A, \quad \sin \alpha=-A_{2} / A$ とおくと、一般解は以下のように書けます。
$$
x=A\left(\frac{A_{1}}{A} \cos \omega t+\frac{A_{2}}{A} \sin \omega t\right)=A(\cos \omega t \cos \alpha-\sin \omega t \sin \alpha)=A \cos (\omega t+\alpha)
$$

ばね・重り系の連成振動

両端が壁に固定され、バネで繋がれた2つの重りの運動を考えます。ばね定数は、$k$、重りの重さは$m$とします。

つりあいの位置からの変位を、$u_1$, $u_2$ とすると、運動方程式は、以下のようになります。
$$
m \ddot{u}_{1}=-k u_{1}-k\left(u_{1}-u_{2}\right) \\\
m \ddot{u}_{2}=-k u_{2}-k\left(u_{2}-u_{1}\right)
$$

$\omega_{0}^{2} \equiv \frac{k}{m}$ とすると、以下のようになります。

$$
\left(\begin{array}{c}
\ddot{u}{1} \\\ \ddot{u}{2}
\end{array}\right)=\omega_{0}^{2}\left(\begin{array}{cc}
-2 & 1 \\\
1 & -2
\end{array}\right)\left(\begin{array}{l}
u_{1} \\\
u_{2}
\end{array}\right)
$$
さらに、$\mathbf{u} \equiv\left(\begin{array}{l}u_{1} \\ u_{2}\end{array}\right), \quad \mathbf{A} \equiv\left(\begin{array}{cc}-2 & 1 \\ 1 & -2\end{array}\right)$ とすると、以下のようになります。

$$
\ddot{\mathbf{u}}=\omega_{0}^{2} \mathbf{A} \mathbf{u}
$$
これを行列 $\mathbf{A}$ の固有値問題として解くと、重りの運動を求めることができる。行列 $\mathbf{A}$ の固有值を $\lambda_{1}, \lambda_{2}$, 固有べクトルを $\mathbf{v}{1}, \mathbf{v}{2}$ とすると,

$$
\mathbf{A} \mathbf{v}_{1}=\lambda_{1} \mathbf{v}_{1} \\
\mathbf{A} \mathbf{v}_{2}=\lambda_{2} \mathbf{v}_{2}
$$
固有方程式を解くと、

$$
\operatorname{det}(\lambda \mathbf{E}-\mathbf{A})=\left|\begin{array}{cc}
\lambda+2 & -1 \\
-1 & \lambda+2
\end{array}\right|=(\lambda+1)(\lambda+3)=0
$$
固有値 $\lambda=-1,-3$ が得られる。固有ベクトル $\mathbf{v}{1}, \mathbf{v}{2}$ として大きさが 1 になるものを選らぶと,

$$
\begin{aligned}
\lambda_{1}=-1 \text { に対して, } & \mathbf{v}{1}=\frac{1}{\sqrt{2}}\left(\begin{array}{l} 1 \\ 1 \end{array}\right) \\ \lambda{2}=-3 \text { に対して, } & \mathbf{v}_{2}=\frac{1}{\sqrt{2}}\left(\begin{array}{c}
1 \\
-1
\end{array}\right)
\end{aligned}
$$
となります。この固有ベクトルを基底として、ベクトル $\mathbf{u}$ を、次のように表します。

$$
\mathbf{u}=a_{1}(t) \mathbf{v}{1}+a{2}(t) \mathbf{v}_{2}
$$
これを上の式に代入すｌると、以下のようになります。

$$
\ddot{a}_{1} \mathbf{v}_{1}+\ddot{a}_{2} \mathbf{v}_{2}=\omega_{0}^{2}\{a_{1} \mathbf{A} \mathbf{v}_{1}+a{2} \mathbf{A} \mathbf{v}_{2}\}
$$

固有値と固有ベクトルの関係を用いると、次のようになります。

$$
\ddot{a}_{1} \mathbf{v}{1}+\ddot{a}_{2} \mathbf{v}{2}=\omega_{0}^{2}\{a_{1} \lambda_{1} \mathbf{v}_{1}+a{2} \lambda_{2} \mathbf{v}_{2}\}
$$
固有ベクトル $\mathbf{v}_{1}, \mathbf{v}_{2}$ の1次独立性をつかって、
$\ddot{a}_{1}-\omega_{0}^{2} \lambda_{1} a_{1}=0, \quad \ddot{a}_{2}-\omega_{0}^{2} \lambda_{2} a_{2}=0$
すなわち、以下のようになります。
$$
a_{1}(t)=\beta_{1} \cos \omega_{0} \sqrt{-\lambda_{1}} t+\gamma_{1} \sin \omega_{0} \sqrt{-\lambda_{1}} t \\
a_{2}(t)=\beta_{2} \cos \omega_{0} \sqrt{-\lambda_{2}} t+\gamma_{2} \sin \omega_{0} \sqrt{-\lambda_{2}} t
$$
$\mathbf{u}=a_{1}(t) \mathbf{v}_{1}+a{2}(t) \mathbf{v}_{2}$ なので、

$$
\begin{gathered}
\mathbf{u}=\left(\begin{array}{l}
u_{1} \\
u_{2}
\end{array}\right)=\left(\beta_{1} \cos \sqrt{\frac{k}{m}} t+\gamma_{1} \sin \sqrt{\frac{k}{m}} t\right) \frac{1}{\sqrt{2}}\left(\begin{array}{l}
1 \\
1
\end{array}\right) \\
+\left(\beta_{2} \cos \sqrt{\frac{3 k}{m}} t+\gamma_{2} \sin \sqrt{\frac{3 k}{m}} t\right) \frac{1}{\sqrt{2}}\left(\begin{array}{c}
1 \\
-1
\end{array}\right)
\end{gathered}
$$
が得られます。各係数は、重りの位置と速度に関する初期条件から決定されます。

まとめると

以上、式の導出はややこしいようですが、何をやっているのかというと、運動方程式
$$
\ddot{\mathbf{u}}=\omega_{0}^{2} \mathbf{A} \mathbf{u}
$$
を、固有値と固有ベクトルの関係と、固有ベクトルの独立性を用いて、
$$
\mathbf{A} \mathbf{v}_{1}=\lambda_{1} \mathbf{v}_{1} \\
\mathbf{A} \mathbf{v}_{2}=\lambda_{2} \mathbf{v}_{2}
$$
固有ベクトルの独立性を使って、成分に分解し、
$$
\mathbf{u}=a_{1}(t) \mathbf{v}{1}+a{2}(t) \mathbf{v}_{2}
$$
独立した2つの方程式にして、それを解いているわけです。
$$
\ddot{a}_{1}-\omega_{0}^{2} \lambda_{1} a_{1}=0 \\
\ddot{a}_{2}-\omega_{0}^{2} \lambda_{2} a_{2}=0
$$
これは、重りが一個のバネ振子の運動方程式と同じ形式です。つまり、重りが２つの場合の連成振動を、重りが一つのバネ振子２つに分離していることになります。
$$\frac{d^{2} x}{d t^{2}}+\omega^{2} x=0$$