テンソルネットワーク
テンソルネットワークは、大きなテンソルを小さなテンソルのネットワークに分解したもので、応用数学、化学、物理学、機械学習など多くの分野で応用されます。また、量子回路シミュレーションは、テンソルネットワークの主要な用途の一つです。すべての量子回路はテンソルネットワークに正確にマッピングできます。テンソルネットワークを完全に縮約した後、結果として得られるテンソルは、測定直前の量子回路の波動関数に等しくなります。
テンソルとは
テンソル(英: tensor, 独: Tensor)とは、線形的な量または線形的な幾何概念を一般化したもので、基底を選べば、多次元の配列として表現できるようなものです。階数$0$のスカラーや階数$1$のベクトル、階数$2$の行列などの階数$n$への一般化を与えているものと見なされます。0次元はスカラー、1次元はベクトル、2次元は配列、そして、3次元以上がテンソルとよばれますが、それらをまとめて考えるのがテンソルです。
https://ja.wikipedia.org/wiki/テンソル
Tensor Diagram Notation (テンソル図表記)
$\sum_{j} M_{i j} N_{j k l}$は、以下のように表記されます。

Tensor Diagram Rules(テンソル図ルール)
- テンソルは立体形状(上の例では、○)で表記され、テンソルの添字は立体形状から伸びる線で表記されます。
- 2つのインデックスを結ぶ線は縮約を意味し、接続されたインデックスに対する和を意味します。
上の例では、$M$ は、$i,j$ をインデックスとするテンソル(配列)、$N$ は、$j, k, l$ をインデックスとするテンソルで、インデックス $j$ に対して和をとるということを表します。
テンソル図の例
次元の低いテンソルの例

行列的な縮約の例

$\operatorname{Tr}[AB]$ は、行列のトレースです。
$$
\begin{aligned}
\operatorname{tr}[A B] &=\sum_{k=1}^{n}(A B)_{k k} =\sum_{k=1}^{n} \sum_{l=1}^{m} a_{k l} b_{l k}
\end{aligned}
$$
テンソルの縮約

単位行列
テンソルをそのインデックスの一つ上で単位行列と縮約しても何の効果もないので、単位行列は他のテンソルのように「形」を持たない単なる線として表記するのが通例です。図式的には次のようになります。

この表記は、単位行列の縮退の図が、単にインデックスの線を拡張するだけ、つまりテンソルに何の影響も与えないので、便利です。

行列積状態/テンソルトレイン (Matrix Product State / Tensor Train)
行列積状態 (MPS)またはテンソル列テンソルネットワークは、N個のインデックスを持つテンソルを3個のインデックスのテンソルの鎖状積に分解するものです。テンソル$T$の行列積状態/テンソル列分解は、テンソル図表記で次のように表すことができます。
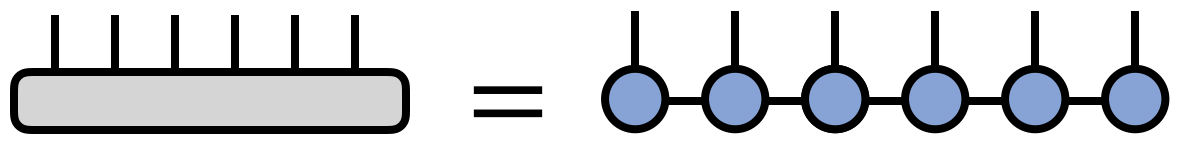
ここで、具体化のためにTは6個のインデックスを持つものとしていますが、上のパターンは任意の数のインデックスを持つテンソルに対して一般化できます。
あるいは、テンソルのMPS/TTの分解(factorization)は、従来の表記法で次のように表すことができます。
$$
T^{s_{1} s_{2} s_{3} s_{4} s_{5} s_{6}}=\sum_{{\alpha}} A_{\alpha_{1}}^{s_{1}} A_{\alpha_{1} \alpha_{2}}^{s_{2}} A_{\alpha_{2} \alpha_{3}}^{s_{3}} A_{\alpha_{3} \alpha_{4}}^{s_{4}} A_{\alpha_{4} \alpha_{5}}^{s_{5}} A_{\alpha_{5}}^{s_{6}}
$$
ここで、結合指標(bond indeces) $α$は縮約されているか、または総和されています。一般に各$A$テンソルは互いに異なることがあることに注意してkださい。異なる文字で表す代わりに、単にインデックスで区別するのが便利です。
どのようなテンソルも、結合指標 $α$の次元が十分大きければ、MPS / TT形式で正確に表現することができます。
結合次元/ランク (Bond Dimension / Rank)
行列積状態やテンソル列分解を理解する上で重要な概念は、結合次元やテンソル列ランクであり、仮想次元とも呼ばれることがあります。これは鎖の中のあるテンソルを次のテンソルに接続する結合インデックスの次元であり、結合ごとに変化しえます。結合次元はMPS/TTネットワークの表現力を制御するパラメータと考えることができます。上の例では、$α$インデックスの次元です。
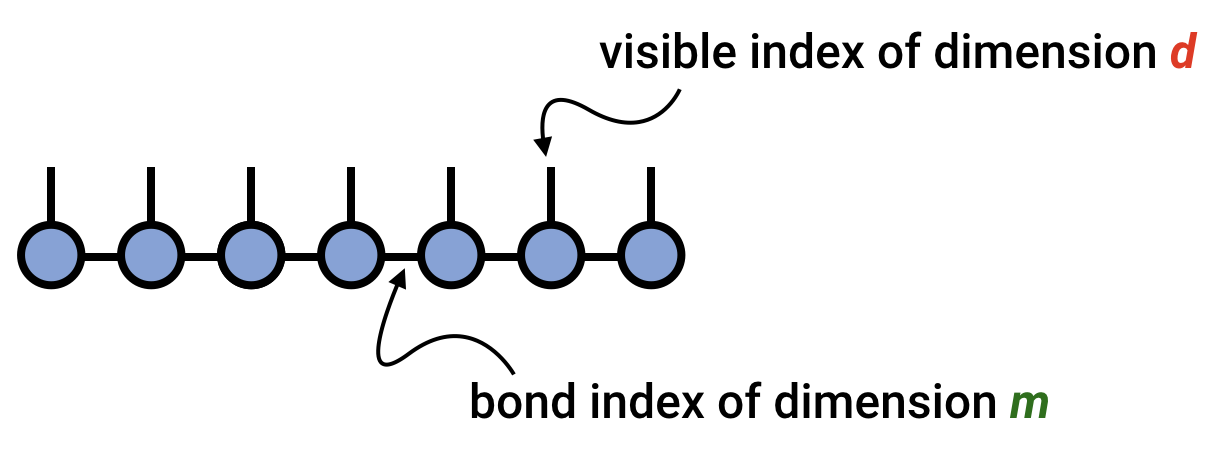
結合次元やランクが十分大きければ、MPS/TTは任意のテンソルを表現することができます。テンソル $T^{s_{1} s_{2}}$ を考えてみまます。$d$ 次元の$\mathrm{N}$インデックスを持つテンソル$T^{s_{1} s_{2} s_{N}}$を考えてみます。するとこのテンソルは常に結合次元$m=d^{N / 2}$のMPS/TTとして正確に表現することができます。
$$
N d m^{2}
$$
この数は、因子テンソルにある種の制約を課すか利用することで、さらに減らすことができます。
もしテンソルのMPS/TT表現が良い近似であれば、$N$に対して指数関数的に増加するパラメータ群から、$N$に対してちょうど線形に増加するパラメータ群へと大幅に圧縮されることを意味します。
MPS/TTのネットワークに内在する冗長性を利用することで、表現力を損なわずにパラメータ数をさらに減らすことが可能です。

