Robust Amplitude Estimation RAE ロバストな振幅推定
| Reducing runtime and error in VQE using deeper and noisier quantum circuits Amara Katabarwa, Alex Kunitsa, Borja Peropadre, Peter Johnson arXiv:2110.10664 , 2021 |
VQEなどのNISQ対応アルゴリズムの高速化の提案です。以下、論文の概要です。
Reducing runtime and error in VQE using deeper and noisier quantum circuits
VQEを含む多くの量子アルゴリズムにおける期待値の推定を、我々が「ロバストな振幅推定」(Robust Amplitude Estimation, RAE)と呼ぶ技術を用いることで、精度と正確さの点で改善できることを、量子ハードウェア上で実証しました。この手法は、標準的な測定推定法と比較して、同じ平均二乗誤差を達成するための実行時間を短縮することができます。驚くべきことに、より深い、つまりより誤差が生じやすい量子回路を用いることで、より正確な量子計算をより短時間で実現できるのです。量子デバイスの品質が向上すれば、この方法は推定の実行時間を比例的に短縮することができます。この手法は、量子計算を早期に耐故障性量子計算の領域まで高速化し、量子的な優位性を実現するために利用できるかもしれません。
本論文では、ロバストな振幅推定が、パウリ期待値の推定効率において、標準的なVQEよりもすでに向上していることを実証しました。多くの場面では、回路全体のエラーレートを10%以下、あるいは1%以下に抑えたいと思うかもしれませんが、今回の研究では、回路全体のエラーレートが40%程度の回路を使用することで、計算時間を最小限に抑えることができます。2つの量子ビットを用いた実験では、ロバストな振幅推定により、同じ実行時間であれば、VQEで一般的に用いられる標準的なサンプリングと比較して、RMSEを4分の1に削減できることを示しています。また,RMSEの低減に加えて,バイアスを10倍に低減することで精度を向上させ,この手法がエラーを軽減する能力があることを示しました.
ロバストな振幅推定では,強化されたサンプリングを用いて,ノイズの多い量子コンピュータでの期待値の推定を高速化しています.VQEなどで用いられる標準的なサンプリング手法とは対照的に,強化されたサンプリング手法は,量子ハードウェアの品質向上に比例して推定実行時間を短縮することができます.ここでは,これらの手法のうち,実験で用いた最も単純な手法を説明します。
多くの量子アルゴリズムでは、以下の期待値を求めることが必要です。
$$
\Pi=\langle A|P| A\rangle
$$
ここで、$A$ は、アンザッツで、$P$ はハミルトニアンです。単純な推定は、状態 $|A\rangle$ を繰り返し、準備して、$P$を測定することです。このやり方を、標準的なサンプリングと呼びます。このやり方は、VQEやその他のNISQ量子アルゴリズムで用いられます。
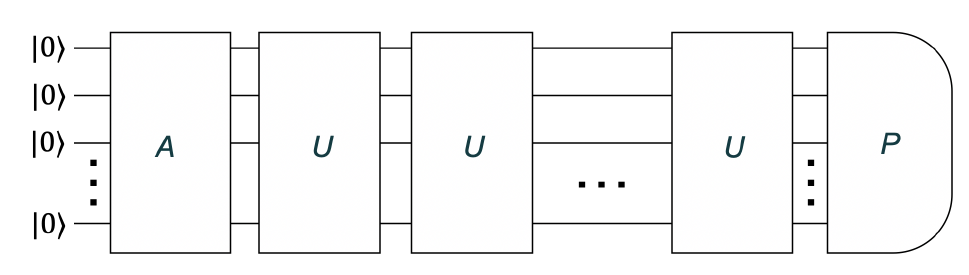
強化されたサンプリングとは,期待値が対象となる期待値の関数となる量子状態からデータを収集するというものです.標準的なサンプリング方法を改良して,アンサッツ状態$|A\rangle=A\left|0^{n}\right\rangle$を用意し,グローバー層 $L$、 $U=A\left(2|0\rangle\left\langle\left. 0\right|^{\otimes n}-\mathbb{I}\right) A^{\dagger} P\right.$ を適用し,パウリ観測量$P$を測定します.この一連の流れを図1に示します。標準的なサンプリングと比較して、実質的に新しく導入された操作は、$R_{0}=2|0\rangle\left\langle\left. 0\right|^{\otimes n}-\mathbb{I}\right.$ だけです。
グローバーのアルゴリズム
$N$ 個の要素からなるデータベースから $M$ 個の解を探索する問題を考え、要素のラベルを $n$ 桁のビット列 $x=x_1…x_n$ とする。
- 全ての状態の重ね合わせ状態 $|s\rangle=\frac{1}{\sqrt{N}} \sum_{x}|x\rangle$ を用意する
初期状態 $|0 \cdots 0\rangle$ に対して全ての量子ビットにアダマールゲート $H$ をかければ良い。
$$
(H \otimes \cdots \otimes H)|0 \cdots 0\rangle=\frac{1}{(\sqrt{2})^{n}}(|0\rangle+|1\rangle) \otimes \cdots \otimes(|0\rangle+|1\rangle)=|s\rangle
$$
- オラクル $U_w$ (解に対する反転操作)を作用させる
次に、オラクルを状態 $|s\rangle$ に作用させる。ここではオラクルとして、前節の最後で述べた ような「入力 $|x\rangle$ に対して $x$ が解なら(-1)をかけて位相を反転し、解でないなら何もしな い」という演算を考える次に、オラクルを状態 $|s\rangle$ に作用させる。ここではオラクルとして、前節の最後で述べた ような「入力 $|x\rangle$ に対して $x$ が解なら(-1)をかけて位相を反転し、解でないなら何もしな い」という演算を考える。オラクル $U_{w}$ を、以下のように定義する。
$$
U_{w}=I-2 \sum_{w \in \text { 解 }}|w\rangle\langle w| \\
U_{w}|x\rangle=|x\rangle(\mathrm{x} \text { is not solution }) \\
U_{w}|x\rangle=-|x\rangle(\mathrm{x} \text { is solution })
$$
入力が解である時にだけ位相を反転させるので、オラクル $U_{w}$ は「解に対す る反転操作」と呼ばれる。 - $|s⟩$ を対称軸にした反転操作 $Us$ を作用させる
ステップ2では解に対する反転操作を考えたが、ステップ3では全ての状態の重ね合わせ $|s\rangle$ を対称軸にした反転操作 $U_{s}$ を作用させる。
$$
U_{s}=2|s\rangle\langle s|-I
$$
この演算子は、入力状態 $|\psi\rangle=a|s\rangle+b\left|s_{\perp}\right\rangle \quad\left(\left|s_{\perp}\right\rangle\right.$ は $|s\rangle$ に直交するベクトル)に対して
$$
U_{s}|\psi\rangle=a|s\rangle-b\left|s_{\perp}\right\rangle
$$
と作用し、 $\left|s_{\perp}\right\rangle$ に比例する部分の位相だけを反転する。 - ステップ 2,3 を $k$ 回繰り返す
上記の2つの反転操作 $U_{w}$ と $U_{s}$ を繰り返す。およそ $O(\sqrt{N / M})$ 回の繰り 返しを行えば、次のステップ5の測定で十分高い確率で解が得られる。つまり、オラクル を呼ぶ回数は $O(\sqrt{N})$ で良い - 測定を行う
ここまでのステップで状態は $\left(U_{s} U_{w}\right)^{k}|s\rangle$ となっている。 $k$ はステップ2,3の繰り返しの回 数である。実はこの状態は、解 $w$ に対応する状態 $|w\rangle$ の係数(の絶対値)のみが非常に大きくなっているので、計算基底で測定を行えば、高い確率で解 $w$ (ビ ット列) が得られる。
注) オラクル (Oracle) は日本語で神託という意味であり、中身はブラックボックスだけれどとにかく答えを教えてくれる抽象的な存在で、それがどのように実装されているかは気にしない(実際に実装が存在する必要もない)。
$L$ を変化させ、その結果から、$\Pi=\langle A|P| A\rangle$ を最尤推定します。
$$
\mathbb{P}(\pm 1 \mid \Pi ; L)=\frac{1}{2}\left(1 \pm T_{2 L+1}(\Pi)\right)
$$
$T_{m}(x)=\cos (m \arccos (x))$ は、m次のチェビシェフ多項式です。
実際には、量子計算には誤差があっても、誤差が尤度関数に与える影響のモデルを推論プロセスに組み込むことで、期待値を推定することができます。モデルの精度が十分に高く、モデルのパラメータを一定の許容範囲内で学習することができれば、目的のパラメータを正確に推定できる可能性があります。そのようなモデルとして、指数減衰モデルを採用しました。
$$
\mathbb{P}(\pm 1 \mid \Pi, \lambda ; L)=\frac{1}{2}\left(1 \pm e^{-(L+1 / 2) \lambda} T_{2 L+1}(\Pi)\right)
$$
$\lambda$ は、減衰パラメータで、量子デバイスの最初のエラー率に比例させます。ここで重要なことは、提案したモデルは、結果の尤度とパラメータの間の実際の関係の近似値であることです。したがって,この研究で扱う重要な問題は ロバストな振幅推定は,この近似モデルを用いた場合,実際にどの程度の性能を発揮するのかということです.
推論プロセス、一回ごとに、 $L$層からのビット出力列 $s=\pm 1$ にもとづいて事前確率 $p(\Pi, \lambda)$ を更新し、次の事後確率を求めます。
$$
p(\Pi, \lambda \mid s)=\frac{\mathbb{P}(s \mid \Pi, \lambda ; L) p(\Pi, \lambda)}{\int d \Pi d \lambda \mathbb{P}(s \mid \Pi, \lambda ; L) p(\Pi, \lambda)}
$$
測定とベイス更新をくりかえし、 事後確率を最大化する$\hat{\Pi}$ と $\hat{\lambda}$をもとめ、これを $\hat{\Pi}$ パラメータの推定値とします。パラメータ $\lambda$ は、 最尤推定値に到達する過程の$\Pi$ の系統誤差(Nuisance Parameter)として扱われます。


