QAOA 問題定式化の課題
QAOAでは、目的関数と制約条件を加えたものをコスト関数として、その最小値を量子断熱計算で求めるものです。「IBM Quantumで学ぶ量子コンピュータ」で紹介せれている交通最適化問題を例に、課題をみてみたいと思います。
コスト関数に制約条件を加えた場合
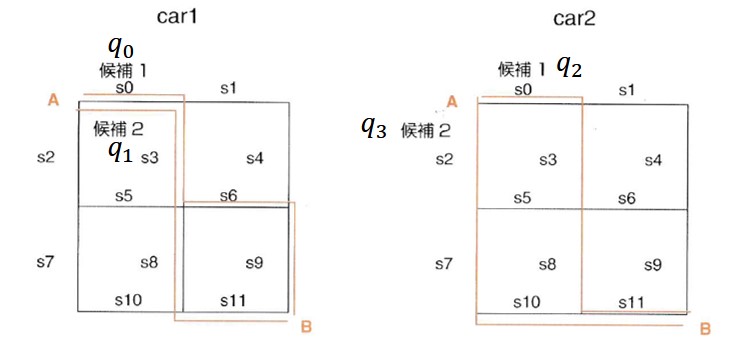
car1とcar2が、2つの経路候補をとるときに、目的関数を、各道をつかう車を足し算したものの二乗で定義される混雑度として、以下のように定式化されています。
$$
4 q_{0}+4 q_{1}+4 q_{2}+4 q_{3}+4 q_{0} q_{1}+4 q_{0} q_{2}+8 q_{1} q_{2}+2 q_{1} q_{3}+2 q_{2} q_{3}
$$
制約条件条件は、ルート選択は一つだけなので、$q_0$か$q_1$の片方が1でもう片方は0が条件になります。$q_2$と$q_3$も同様です。
$q_i$は、0か1なので、$q_i^2=q_i$ という関係を用いて変形すると、制約条件は、以下のようになります。
$$
\begin{array}{l}
(q_0 + q_1 – 1)^2 + (q_2 + q_3 – 1)^2 \\\
= 2q_0q_1 -q_0-q_1+1 + 2q_2q_3 -q_2-q_3+1
\end{array}
$$
コスト関数は、目的関数と制約条件を足し合わせて、以下のようになります。
$$
\begin{array}{l}4 q_{0}+4 q_{1}+4 q_{2}+4 q_{3}+4 q_{0} q_{1}+4 q_{0} q_{2}+8 q_{1} q_{2}+2 q_{1} q_{3}+2 q_{2} q_{3} + \\\
c(2q_0q_1 -q_0-q_1+1 + 2q_2q_3 -q_2-q_3+1))
\end{array}
$$
これを、qiskitを用いてプログラムすると以下のようになります。
from qiskit.optimization import QuadraticProgram
c = 6
qubo = QuadraticProgram()
qubo.binary_var('q0')
qubo.binary_var('q1')
qubo.binary_var('q2')
qubo.binary_var('q3')
linear = {'q0': 4 - c, 'q1': 4 - c , 'q2': 4 - c, 'q3': 4 - c }
quadratic = {('q0', 'q1'): 4 + 2 * c, ('q0', 'q2'): 4, ('q1', 'q2'): 8, ('q1', 'q3'): 2, ('q2', 'q3'): 2 + 2 * c}
qubo.minimize(linear=linear, quadratic=quadratic)
print(qubo)
from qiskit import Aer
from qiskit import QuantumCircuit, execute
from qiskit.aqua.operators import I, X, Y
from qiskit.aqua.components.initial_states import Custom
from qiskit.optimization.algorithms import MinimumEigenOptimizer
from qiskit.aqua import QuantumInstance
from qiskit.aqua.algorithms import QAOA
quantum_instance = QuantumInstance(Aer.get_backend('statevector_simulator'))
step = 1
qaoa_mes = QAOA(quantum_instance=quantum_instance, p=step)
qaoa = MinimumEigenOptimizer(qaoa_mes)
qaoa_result = qaoa.solve(qubo)
print(qaoa_result)
ここで問題になるのが、ハイパーパラメータ c をどう決めるかです。
上のプログラムでは、c = 6 とすると、以下のように、[1. 0. 0. 1.] と正しい答えがでます。
Minimize
obj: - 2 q0 - 2 q1 - 2 q2 - 2 q3 + [ 32 q0*q1 + 8 q0*q2 + 16 q1*q2 + 4 q1*q3
+ 28 q2*q3 ]/2
Subject To
Bounds
0 <= q0 <= 1
0 <= q1 <= 1
0 <= q2 <= 1
0 <= q3 <= 1
Binaries
q0 q1 q2 q3
End
optimal function value: -4.0
optimal value: [1. 0. 0. 1.]
status: SUCCESS
c を4以下にすると、[0. 0. 0. 0.]、つまりどのルートも選ばれないという結果になります。
例えば、c = 2 にすると、コスト関数は以下のようになり、$q_i$ は、すべて0 が最適解として選ばれるからです。
obj: 2 q0 + 2 q1 + 2 q2 + 2 q3 + [ 16 q0*q1 + 8 q0*q2 + 16 q1*q2 + 4 q1*q3 + 12 q2*q3 ]/2
Traffic Flow Optimization using the D-Wave Quantum Annealer に、この問題が紹介されていますが、そのなかにも、制約条件のハイパーパラメータについて、以下の記述があります。
The magnitude of the penalty term, K, is tuned based on the size of the problem
(i.e. violating one constraint increases the energy of the state as if one more car was
present on every road segment)
このように、QAOAで組み合わせ最適化問題を定式化して解くときに、制約条件をコスト関数にくわえる場合、制約条件にかける係数の決め方には、注意が必要です。このブログの
QAOAの応用(問題の定式化)でも、いろんな定式化を紹介していますが、同じ状況にあり、十分な検討が必要であると考えています。
つまり、目的関数に係数をかけた制約条件を加えてコスト関数にしているため、目的関数と制約条件のバランスに注意する必要があるということです。
ミキサーを用いた場合
コスト関数に制約条件を加えた場合に生じる課題を解決する一つの手法として、「IBM Quantumで学ぶ量子コンピュータ」では、ミキサーがもちいた分析がされています。QAOAでは、量子ビットの初期状態として、各量子ビットに、アダマールゲートをかけ初期状態が作られますが、この初期状態を問題を解くのに適当な状態にすることが考えられます。これは、ミキサーと呼ばれます。
制約条件条件は、ルート選択は一つだけなので、q0かq1の片方が1でもう片方は0が条件なので、以下のようなミキサーが指定されています。
$$
\frac{X \otimes X+Y \otimes Y}{2}
$$
固有状態は、以下の通りです。
$$
\frac{1}{\sqrt{2}}(|01\rangle+|10\rangle)
$$
つまり、初期状態として、$q_0$あるいは$q_1$の片方が1である状態をつくり、そこから量子断熱計算をしていくということです。プログラムは、以下の通りです。
from qiskit.optimization import QuadraticProgram
qubo = QuadraticProgram()
qubo.binary_var('q0')
qubo.binary_var('q1')
qubo.binary_var('q2')
qubo.binary_var('q3')
linear = {'q0': 4, 'q1': 4, 'q2': 4, 'q3': 4}
quadratic = {('q0', 'q1'): 4, ('q0', 'q2'): 4, ('q1', 'q2'): 8, ('q1', 'q3'): 2, ('q2', 'q3'): 2}
qubo.minimize(linear=linear, quadratic=quadratic)
print(qubo)
from qiskit import Aer
from qiskit import QuantumCircuit, execute
from qiskit.aqua.operators import I, X, Y
from qiskit.aqua.components.initial_states import Custom
mixer = ((X^X^I^I)+(Y^Y^I^I))/2 + ((I^I^X^X) + (I^I^Y^Y))/2
initial_state_circuit = QuantumCircuit(4)
initial_state_circuit.h(0)
initial_state_circuit.cx(0, 1)
initial_state_circuit.x(0)
initial_state_circuit.h(2)
initial_state_circuit.cx(2, 3)
initial_state_circuit.x(2)
initial_state_vec = execute(initial_state_circuit, Aer.get_backend('statevector_simulator')).result().get_statevector()
initial_state = Custom(4, state_vector=initial_state_vec)
from qiskit.optimization.algorithms import MinimumEigenOptimizer
from qiskit.aqua import QuantumInstance
from qiskit.aqua.algorithms import QAOA
quantum_instance = QuantumInstance(Aer.get_backend('statevector_simulator'))
step = 1
qaoa_mes = QAOA(quantum_instance=quantum_instance, p=step, initial_state=initial_state, mixer=mixer)
qaoa = MinimumEigenOptimizer(qaoa_mes)
qaoa_result = qaoa.solve(qubo)
print(qaoa_result)
print('no mixer')
quantum_instance = QuantumInstance(Aer.get_backend('statevector_simulator'))
step = 1
qaoa_mes = QAOA(quantum_instance=quantum_instance, p=step)
qaoa = MinimumEigenOptimizer(qaoa_mes)
qaoa_result = qaoa.solve(qubo)
print(qaoa_result)
次のようなコスト関数に対して、正しい結果が得られています。
Minimize
obj: 4 q0 + 4 q1 + 4 q2 + 4 q3 + [ 8 q0*q1 + 8 q0*q2 + 16 q1*q2 + 4 q1*q3
+ 4 q2*q3 ]/2
optimal function value: 8.0
optimal value: [1. 0. 0. 1.]
当たり前ですが、ミキサーをなくすと、解はすべて0になってもとまりません。上のコスト関数をみてっも、各項の係数がすべて正になっていることからも、こうなるのがわかります。
optimal function value: 0.0 optimal value: [0. 0. 0. 0.]


