5月 7, 2021 / 最終更新日時 : 5月 7, 2021 Koichi Tsujino いちから始める量子コンピュータ

VQEを使って配車ルート問題を解く

ここでは、IBM Quantum Lab から Qiskit_tutorials/qiskit/optimazation/07_examples_vehicle routing 配車ルート問題の解法を紹介します。このURLにアクセスするには、IBM Quantum ユーザ登録が必要です。

登録方法 IBM Quantum Composerの登録

はじめに

ほとんどの物流業者は、多数の車、多数の拠点を運営しています。重要な課題は、車両の走行距離、時間などを最小限に抑えるために、拠点から多数の配送先に行って拠点に戻るルートをどのようにとるかです。ここでは、問題の理想化されたかたちで形式化し、Farhi、Goldstone、およびGutmann（2014）の量子近似最適化アプローチを使用してその解法を紹介します。

配送先をを確定します。通常、配送日の前に確定可能が、ここでは、これらをランダムに生成します。
配送先の二点間の距離、移動時間などを計算します。ここでは、ユークリッド距離を使います。
実際のルートを計算します。最初は、古典的なコンピューターで古典的なソルバー（IBM CPLEX）をもちいます。次に、量子コンピューターをもちいた量子古典ハイブリッドアルゴリズムで計算します。
結果の視覚化を行います。

モデル

数学的には、車両ルート問題（VRP）は組み合わせ問題であり、利用可能な車両の数を考慮して、拠点から多数の配送先に行き、拠点に戻る最適なルートが求めるものです。ここでは、セールスマン巡回問題を拡張したMTZ [Miller、Tucker、Zemlin、1960]として知られる定式化を紹介します。

$n$を配送先の数($1,…,n$)、$K$を車両の数、$x_{ij}=\{0,1\}$を、1ならばノード $i$ からノード$j$を活性化する２値の決定変数とします。ノードのインデックス 0 を拠点とします。

２つのノード $i$ と $j$が、$i$から$j$へのリンクをもつとき、$i \sim j$と記述します。
ノード$i$が、リンクをもつノードの集合を、$\delta(i)^+$ すなわち　$i \sim j$ のみを持つ場合、 $j \in \delta(i)^+$ と記述します。同様に、$\delta(i)^-$を、$i$に結合されているノードの集合とします。

さらに、ノード($i = 1,…,n$)に対して連続変数 $u_i$を考えます。これは、MTZによる定式化で、部分順回路除去 (eliminate sub-tours between clients) のために必要です。

VRPは、以下のように定式化できます。

$$
(V R P) \quad f=\min_{\{x_{i j}\}_{i \sim j} \in{0,1},\{u_{i}\}_{i=1, \ldots, n \in \mathbb{R}}} \sum_{i \sim j} w_{i j} x_{i j}
$$

すでに訪れた配送先への制約条件

$$
\sum_{j \in \delta(i)^{+}} x_{i j}=1 \\\ \sum_{j \in \delta(i)^{-}} x_{j i}=1, \ \forall i \in{1, \ldots, n}
$$

拠点の制約条件

$$ \sum_{i \in \delta(0)^{+}} x_{0 i}=K, \ \sum_{j \in \delta(0)^{+}} x_{j 0}=K $$

部分順回路除去制約条件

$$
u_{i}-u_{j}+Q x_{i j} \leq Q-q_{j}, \ \forall i \sim j, i, j \neq 0, \ \quad q_{i} \leq u_{i} \leq Q, \ \forall i, i \neq 0
$$

コスト関数は線形で、正の重み $w_{ij} > 0$ （典型的には、ノード間の距離）で決まります。
最初の制約条件は、配送先へのリンクが一つのみが許されるということです。
第二の制約条件は、拠点へのリンクは、ちょうど$K$だけが許されるということです。
第三の制約条件は、部分順回路を除去する条件で、 $Q>q_{j}>0$, and $Q, q_{i} \in \mathbb{R}$となる$u_{i}$で制約されます。

部分順回路除去 (sub-tour eliminate）

以下の配送先の制約条件だけでは、一部の配送先だけを巡回する部分順回路ができてしまうため、その制約条件が必要です。

$$
\sum_{j \in \delta(i)^{+}} x_{i j}=1 \\\ \sum_{j \in \delta(i)^{-}} x_{j i}=1, \ \forall i \in{1, \ldots, n}
$$

部分順回路の例

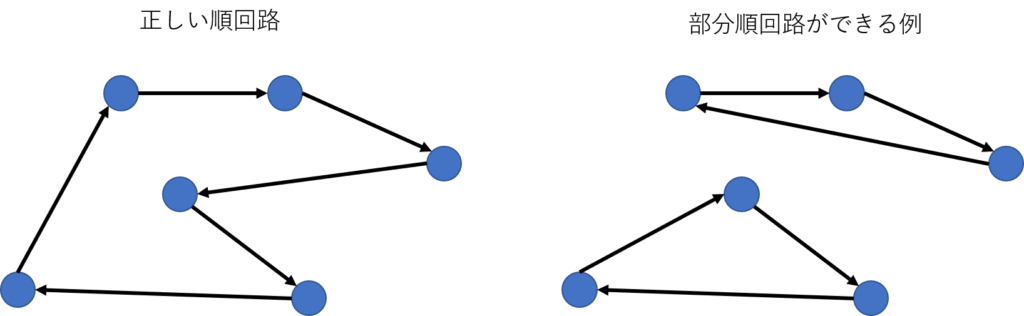
各配送先へのリンクと各配送先からのリンクは、１ですが、右の例にあるように、部分的な配送先を巡回する巡回路も、この条件を満たします。

古典コンピュータによる解

決定変数を、一つのベクトルにして、mixed-integer linear program (MILP)という手法で解きます。

$$
\mathbf{z}=\left[x_{01}, x_{02}, \ldots, x_{10}, x_{12}, \ldots, x_{n(n-1)}\right]^{T}
$$

ここで、$\mathbf{z} \in\{0,1\}^{N}$, with $N=n(n+1)$ です。

演算時間は、ノード数にたいして二次関数的に増大します。

$\mathbf{z}^{*}$を、最適コスト$f^{*}$ をもつ最適解とします。

量子コンピュータによる解

ここでは、Farhi、Goldstone、およびGutmann（2014）の量子近似最適化アプローチに従って、古典的なコンピューティングステップと量子コンピューティングステップを組み合わせたアプローチを示します。特に、変分量子固有値ソルバー（VQE）を使用します。使用される量子回路の深さが限られていることを考えると、得られる解は本質的にヒューリスティックであるため、アルゴリズムの高速化について説明するのは困難です。

アルゴリズムは、以下のように要約できます。

準備段階
- 組み合わせ問題を、バイナリ多項式最適化問題に変換します。
- 結果を、必要に応じてペナルティ法を使用して、変数$\boldsymbol{z}$および基底$\boldsymbol{𝑍}$のイジングハミルトニアン（$H$）にマッピングします。
- 量子回路の深さ $m$ を選択します。
- $\theta$をパラメータとする関数$|\psi(\boldsymbol{\theta})\rangle$ を、C-Phase ゲートとY回転ゲートをもちいて作成します。
アルゴリズム
- $C(\theta)=\langle\psi(\theta)|H| \psi(\theta)\rangle$ を、回路出力をZ軸でサンプリングし、イジング項の期待値を合成することで求めます。
- 古典コンピュータのオプティマイザで、新しいパラメータを選択します。
- 解 $\theta^{*}$ に十分近くなるように、$C(\theta)$が最小値に達するまで繰り返します。
- 最後の$\theta$をもちいて、分布 $\left|\left\langle z_{i} \mid \psi(\theta)\right\rangle\right|^{2}　\ \forall i$から解を求めます。

全体を通じて、パラメータはたくさんあり、波動関数の選択には、以下のような関係を考慮します。

$$
|\psi(\theta)\rangle=\left[U_{\text {single }}(\theta) U_{\text {entangler }}\right]^{m}|+\rangle
$$

$U_{\text {entangler }}$　は、C-Phase ゲートのコレクション、$U_{\text {single }}(\theta)=\prod_{i=1}^{N} Y\left(\theta_{i}\right)$　$N$ は、量子ビットの数、$ｍ$は、量子回路の深さです。

イジング・ハミルトニアンの作成

VRP から、$K = n-1$ の場合だけを考えたバイナリ多項式最適化を行うことができます。この場合、部分巡回路除去(sub-tour elimination) は、必要なく、$\boldsymbol{z}$だけが問題の対象です。つまり上の部分順回路除去条件は考慮する必要ないということです。また、$K = n -1$ ですから、配送先の数だけ、車があるという単純な例です。直感的に、各車両は、配送先へ行って帰ってくるというのが、解であることが想像できます。

ハミルトニアンは、以下のように書くことができます。

$(I H) \displaystyle \quad H= \sum_{i \sim j} w_{i j} x_{i j}+A \sum_{i \in\{1, \ldots, n\}}\left(\sum_{j \in \delta(i)^{+}} x_{i j}-1\right)^{2}$

$\displaystyle +A \sum_{i \in \{1, \ldots, n\}}\left(\sum_{j \in \delta(i)^{-}} x_{j i}-1\right)^{2} +A\left(\sum_{i \in \delta(0)^{+}} x_{0 i}-K\right)^{2}+A\left(\sum_{j \in \delta(0)^{+}} x_{j 0}-K\right)^{2} $

ここで、$A$は、十分大きなパラメータです。

ハミルトニアンからQP定式化

ベクトル$\boldsymbol z$と$\delta(i)^{+}=\delta(i)^{-}={0,1, \ldots, i-1, i+1, \ldots, n}$を用いると、ハミルトニアン $H$は、以下のように書けます。

$$
\min_{\mathbf{z} \in{0,1}^{(n+1)}} \mathbf{w}^{T} \mathbf{z}+A \sum_{i \in{1, \ldots, n}}\left(\mathbf{e}{i} \otimes \mathbf{1}_{n}^{T} \mathbf{z}-1\right)^{2}$$

$$+A \sum_{i \in{1, \ldots, n}}\left(\mathbf{v}_{i}^{T} \mathbf{z}-1\right)^{2}+A\left(\left(\mathbf{e}_{0} \otimes \mathbf{1}_{n}\right)^{T} \mathbf{z}-K\right)^{2}+A\left(\mathbf{v}_{0}^{T} \mathbf{z}-K\right)^{2}
$$

すなわち

$$
\min_{\mathbf{z} \in{\mathbf{0}, \mathbf{1}}^{\mathrm{n}(\mathbf{n}+1)}} \mathbf{z}^{\mathrm{T}} \mathbf{Q} \mathbf{z}+\mathbf{g}^{\mathbf{T}} \mathbf{z}+\mathbf{c}
$$

第一項は

$$
\mathbf{Q}=A \sum_{i \in{0,1, \ldots, n}}\left[\left(\mathbf{e}_{i} \otimes \mathbf{1}_{n}\right)\left(\mathbf{e}_{i} \otimes \mathbf{1}_{n}\right)^{T}+\mathbf{v}_{i} \mathbf{v}_{i}^{T}\right]
$$

第二項は

$$
\mathbf{g}=\mathbf{w}-2 A \sum_{i \in{1, \ldots, n}}\left[\left(\mathbf{e}{i} \otimes \mathbf{1}_{n}\right)+\mathbf{v}_{i}\right]-2 A K\left[\left(\mathbf{e}{0} \otimes \mathbf{1}_{n}\right)+\mathbf{v}_{0}\right]
$$

第三項は

$$
c=2 A n+2 A K^{2}
$$

これで、イジングハミルトニアンのQP定式化をしたことで、VQEを使って問題を解く準備ができました。

プログラムの詳細は、IBM Quatum Lab のTutorial をみてもらうとして、ここでは、概要をみていきます。

QP定式化

二次計画法

二次計画法（にじけいかくほう、英: quadratic programming, QP）は、数理最適化における非線形計画法の代表例の一つであり、いくつかの変数からなる二次関数を線形制約の下で最適化（最小化ないしは最大化）する方法である。二次計画法の対象となる最適化問題を二次計画問題という。

問題

拠点も含むノードの数 n = 3
車両の数 K = 2

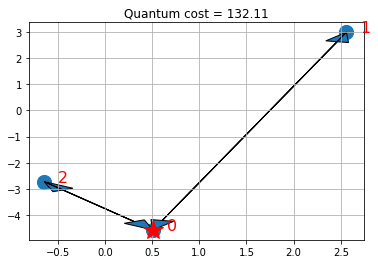
ノートの数は、拠点も含めて、３箇所、車両の台数は２という小さな問題です。そして、二次元空間にノードをランダムに配置して、その間の距離が求められています。

x座標 [0.51003914,  2.55963937, -0.64283509]
y座標 [-4.57068577,  2.98724481, -2.72584275]
ノード間の距離
[[ 0.        , 61.3231758 ,  4.73256478],
 [61.3231758 ,  0.        , 42.89521208],
 [ 4.73256478, 42.89521208,  0.        ]]

図で示すとこのようになります。

古典コンピュータによる解

IBM ILOG CPLEX を使って解くとされていますが、残念ながら、CPLEXが使えませんので、ここでは省略します。

量子コンピュータによる解

QuantumOptimizer とうクラスが作成されています。

binary_representation では、問題をバイナリ表現に変換されています。
construct_problemでは、QUBO 最適化問題を作成されています。
solve_problem では、VQEを使って、問題が解かれています。

from qiskit_optimization import QuadraticProgram
from qiskit_optimization.algorithms import MinimumEigenOptimizer


class QuantumOptimizer:

    def __init__(self, instance, n, K):

        self.instance = instance
        self.n = n
        self.K = K

    def binary_representation(self,x_sol=0):

        instance = self.instance
        n = self.n
        K = self.K

        A = np.max(instance) * 100  # A parameter of cost function

        # Determine the weights w
        instance_vec = instance.reshape(n ** 2)
        w_list = [instance_vec[x] for x in range(n ** 2) if instance_vec[x] > 0]
        w = np.zeros(n * (n - 1))
        for ii in range(len(w_list)):
            w[ii] = w_list[ii]

        # Some variables I will use
        Id_n = np.eye(n)
        Im_n_1 = np.ones([n - 1, n - 1])
        Iv_n_1 = np.ones(n)
        Iv_n_1[0] = 0
        Iv_n = np.ones(n-1)
        neg_Iv_n_1 = np.ones(n) - Iv_n_1

        v = np.zeros([n, n*(n-1)])
        for ii in range(n):
            count = ii-1
            for jj in range(n*(n-1)):

                if jj//(n-1) == ii:
                    count = ii

                if jj//(n-1) != ii and jj%(n-1) == count:
                    v[ii][jj] = 1.

        vn = np.sum(v[1:], axis=0)

        # Q defines the interactions between variables
        Q = A*(np.kron(Id_n, Im_n_1) + np.dot(v.T, v))

        # g defines the contribution from the individual variables
        g = w - 2 * A * (np.kron(Iv_n_1,Iv_n) + vn.T) - \
                2 * A * K * (np.kron(neg_Iv_n_1, Iv_n) + v[0].T)

        # c is the constant offset
        c = 2 * A * (n-1) + 2 * A * (K ** 2)

        try:
            max(x_sol)
            # Evaluates the cost distance from a binary representation of a path
            fun = lambda x: np.dot(np.around(x), np.dot(Q, np.around(x))) \
                  + np.dot(g, np.around(x)) + c
            cost = fun(x_sol)
        except:
            cost = 0

        return Q, g, c, cost

    def construct_problem(self, Q, g, c) -> QuadraticProgram:
        qp = QuadraticProgram()
        for i in range(n * (n - 1)):
            qp.binary_var(str(i))
        qp.objective.quadratic = Q
        qp.objective.linear = g
        qp.objective.constant = c
        return qp
    
    def solve_problem(self, qp):
        algorithm_globals.random_seed = 10598
        quantum_instance = QuantumInstance(BasicAer.get_backend('qasm_simulator'),
                                           seed_simulator=algorithm_globals.random_seed,
                                           seed_transpiler=algorithm_globals.random_seed)

        vqe = VQE(quantum_instance=quantum_instance)
        optimizer = MinimumEigenOptimizer(min_eigen_solver=vqe)
        result = optimizer.solve(qp)
        # compute cost of the obtained result
        _,_,_,level = self.binary_representation(x_sol=result.x)
        return result.x, leve

このクラスを使って、

インスタンスの作成
問題をバイナリ形式に変換
問題を、QuadraticProgramのインスタンスとしてエンコード
問題を解く。量子ビット数にも依存しますが、１２Qビットでは、１２時間以上かかるということです。
[1. 1. 1. 0. 1. 0.] 132.11148115684045
結果を図で表すと以下のようになります。
このような単純な問題ですから、直感的にもわかるように、２台の車で、おのおのの配送先へ行って、帰ってくるという解になっています。

カテゴリー: いちから始める量子コンピュータ、ブログ

VQEを使って配車ルート問題を解く

はじめに