量子アルゴリズム QAA、イジングモデル、QUBO

QAA

QAOA（Quantum Approximate Optimazation Algorithm）に用いられている量子断熱計算(QAA：Quantum Adiabatic Algorithm)について、量子コンピュータの応用 – QAOAの仕組みとこれを応用した組合せ最適化問題のプログラミング(blueqat編)に書かれているQAAの部分をまとめてみます。

量子断熱計算とは、外部からの熱の出入りがない状態を保ちながら、時間をかけてゆっくりと状態変化させることを言います。

$$
\begin{array}{l}
H(t)=\frac{t}{\tau} H_{0}+\left(1-\frac{t}{\tau}\right) H_{I N I} \ \ \cdots \ (1)\\
H_{0}=-\sum_{<i, j>} J_{i j} \sigma_{i}^{z} \sigma_{j}^{z} \ \ \cdots (2)\ \\
H_{I N I}=-\sum_{i=1}^{N} \sigma_{i}^{x} \ \ \cdots \ (3)
\end{array}
$$

ハミルトニアン$(3)$の初期状態から、ハミルトニアン$(2)$の最終状態に向かって、$(1)$にしたがって、状態が遷移してきます。
$H_{I N I}$は、状態ベクトルをニュートラルな状態に置くためパウリ行列の$x$成分$\sigma^{x}$がもちいられます。
パウリ行列の$x$成分$\sigma^x$の固有ベクトルは、以下のようになり、$|0\rangle$と$|1\rangle$の重ね合わせになります。

$$
\begin{array}{l}
|\psi\rangle=\left(\begin{array}{l}
1 \\
1
\end{array}\right) \\
\text { または } \\
|\psi\rangle=\left(\begin{array}{c}
1 \\
-1
\end{array}\right)
\end{array}
$$

また、以下のように書くこともできます。

$$
\begin{array}{l}
|\psi\rangle=|+\rangle=\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle) \\
\text { または } \\
|\psi\rangle=|-\rangle=\frac{1}{\sqrt{2}}(|0\rangle-|1\rangle)
\end{array}
$$

最終状態$H_{0}$は、パウリ行列の$z$成分、$\sigma^z$をかけ合わせた形で、イジングモデルの定義と同じ形式です。
$$H_{0}=-\sum_{<i, j>} J_{i j} \sigma_{i}^{z} \sigma_{j}^{z}$$
パウリ行列の$z$成分についての固有値と固有ベクトルは、

$$
\begin{aligned}
&\text { 固有ベクトルが }|\psi\rangle=\left(\begin{array}{l}
1 \\
0
\end{array}\right) \text { の場合、固有值は 1}\\
\\
&\text { 固有ベクトルが }|\psi\rangle=\left(\begin{array}{l}
0 \\
1
\end{array}\right) \text { の場合、固有值は -1}
\end{aligned}
$$
$H_0$を展開すると、以下のようになります。

$$
H_{0}=-J_{12} \sigma_{1}^{z} \sigma_{2}^{z}-J_{13} \sigma_{1}^{z} \sigma_{3}^{z}-J_{14} \sigma_{1}^{z} \sigma_{4}^{z} \ldots
$$

各インデックス$i,j$それぞれにおいて、固有値が1または-1となり、状態ベクトルも定まります。このことを利用し、パウリ行列のz成分と固有値(±1どちらかを取る)及び固有ベクトルを利用することで、最終状態の状態ベクトルを定め、最終的に組合せ最適解を導くことができます。

量子断熱計算を用いてQAOAを定義するやりかたについては、元の資料量子コンピュータの応用 – QAOAの仕組みとこれを応用した組合せ最適化問題のプログラミング(blueqat編) に詳しく書かれています

イジングモデル

イジングモデルは、小さな磁石を格子状にならべたもので、磁石の上向きを、$|0\rangle$、下向きを、$|1\rangle$とすると、磁石は１量子ビットと考えられます。

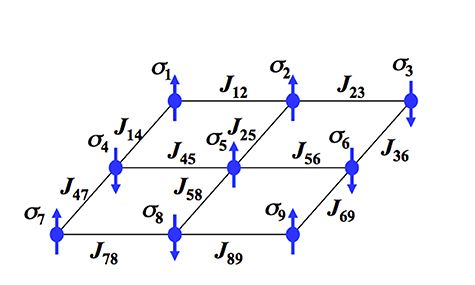
この格子に、横磁場をかけた状態が、量子断熱計算の初期状態$H_{INI}$にあたります。
縦磁場や相互作用を、ハミルトニアンで記述し、徐々に変化させていくことによって、最終状態の最もエネルギーの低い状態を求めるのが、QAOAです。

QUBO

最適化問題とイジングモデルのハミルトニアンの間を対応ずけ、理解しやすいQUBO(Quadratic Unconstrained Binary Optimization)という形式があります。QUBOで、最適化問題を定式化すれば、イジングモデルに変換することができます。
０か１かの値をとる、$n$個の変数 $q_0,q_1,\cdots,q_{n-1}$について、

$$
\sum_{i \leq j} c_{i j} q_{i} q_{j}
$$
を最小化するという形で定式化します。

$c_{ij}$ がプラスなら、$x_i$ と $x_j$ のどちらかが０が望ましい。
$c_{ij}$ がマイナスなら、$x_i$ と $x_j$ の両方１が望ましい。
「AかつB」が望ましいなら、$c_{AB}x_Ax_B$ の項がマイナスになるのが望ましい。
「AまたはB」が望ましいなら、$c_{A A}=c_{B B}=-t, c_{A B}=t, t>0$ として、$c_{A A} x_{A}+c_{B B} x_{B}+c_{A B} x_{A} x_{B}=-t x_{A}-t x_{B}+t x_{A} x_{B}$ とすればよい。
「A、B、Cのどれか一つを選ぶ」という条件は、$\left(x_{A}+x_{B}+x_{C}-1\right)^{2}=0$ となればいいので、$t>0$ として、$t\left(x_{A}+x_{B}+\right.\left.x_{C}-1\right)^{2}=2 t x_{A} x_{B}+2 t x_{A} x_{C}+2 t x_{B} x_{C}$ となるようにパラメータを選べばよい。

などとすることにより問題の定式化をします。

$q_{i}=\frac{1-\sigma_{i}^{z}}{2}$と置くと、QUBOをイジングモデルに変換できます。