量子アルゴリズム QAOA
QAOA は、Quantum Approximate Optimazation Algorithm の略で、量子近似最適化アルゴリズムと呼ばれるものです。以下のように、いろんな説明がされてます。
- 組み合わせ最適化問題の解を求めるためのアルゴリズムです。
- 量子断熱計算を近似した最適化計算が行えます。
理論的にはかなり複雑なものですので、ここでは、直感的な説明を試みます。
まず、blueqatの湊さん等が書かれたIBM Quantum で学ぶ量子コンピュータのQAOAのページをみてみましょう。
量子断熱計算を量子ゲートで近似する
量子断熱計算は、どのような量子状態が最小のエネルギーを取るのかが明らかなハ ミルトニアンから、徐々にハミルトニアンを変化させて、どのような量子状態で最小の エネルギーとなるかわからないような問題を解く量子計算です。
D-Waveに代表される量子アニーラは量子断熱計算を行うことで問題を解いていま す。
量子回路でも、ハミルトニアンに鈴木トロッター展開とよばれる数式展開を行うこ とで量子断熱計算はできるのですが、そのためにたくさんの量子ゲートが必要になり、誤りの多い現在の量子コンピュータではうまく動作しません。
そこで、QAOAという 手法が開発されました。QAOAでは、量子ゲート数は、量子断熱計算をそのまま行うよりも少なくなりますが、そのかわり、PQC(パラメータ付き量子回路)となるため、パラメータの探索が必要で す。
また、東工大西森教授の 量子アニーリング 西森秀稔 では、量子アニーリングは、以下のように説明されています。
目的関数を2値変数の関数(イジング模型)として表現し、その関数の最小値を求める問題として定式化しなければならない。
量子アニーリングを実行するためには、まず目的関数を2値変数の関数(イジング模型)として表現し、その関数の最小値を求める問題として定式化しなければならない。
その目的関数に量子効果を現す項を追加する。
最初に量子項の係数を大きく取り、すべての許される解候補を同じ重みで重ね合わせた状態(下の図の左側)を実現する。
そして、ゆっくりと量子項の係数を小さくしていく。このプロセスにより、容易に実現できる初期状態から出発して、自然な時間変化を経て、下の図の右側のように最適解を高い確率で実現することを目指す。
量子アニーリング 西森秀稔
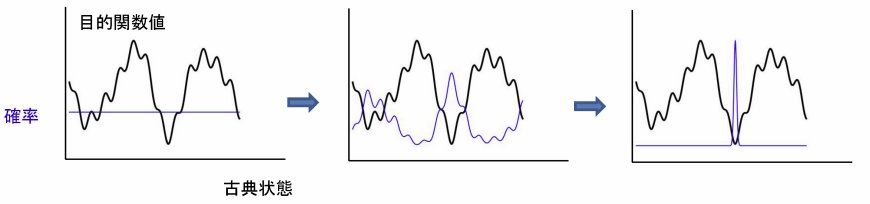
左の初期状態から始めて、シュレディンガー方程式に従って自然な時間発展をしたのち、右の最終状態に行き着く。
Quantum Native Dojo 5-3. Quantum Approximate Optimazation Algorithm (QAOA): 量子近似最適化アルゴリズム では、以下のように説明されています。
問題設定
QAOAでは、$z=z1z2⋯zn(zi=0,1)$ という$n$桁のビット列$z$に関して、コスト関数$C(z)=∑_αC_α(z)$が最小になるような$z$を探す問題を考える。$C_α(z)$はビット列$z$を引数にとる何らかの関数で、ここでは特に、イジングモデル的な$C_α(z)=z_i⋅z_j$といった項を考えれば良い。
この最小化問題を解くために、$n$ビットの量子系を用いる。そして、
$\beta=\left(\beta^{(1)}, \cdots \beta^{(p)}\right), \gamma=\left(\gamma^{(1)}, \cdots \gamma^{(p)}\right)$をパラメータとして、次のような量子状態を考える。
$$|s\rangle=|+\rangle^{\otimes n}=\frac{1}{2^{n / 2}} \sum_{z=0}^{2^{n}-1}|z\rangle $$ $$|\beta, \gamma\rangle=U_{X}\left(\beta^{(p)}\right) U_{C}\left(\gamma^{(p)}\right) \cdots U_{X}\left(\beta^{(1)}\right) U_{C}\left(\gamma^{(1)}\right)|s\rangle$$ここで $|+⟩=1√2(|0⟩+|1⟩)$は$X$演算子の固有状態$X|+⟩=|+⟩$であり、 $UC(γ),UX(β)$ は次のように定義される。
$$U_{C}\left(\gamma^{(i)}\right)=e^{-i \gamma^{(i)} C(Z)}=\prod_{\alpha} e^{-i \gamma^{(i)} C_{\alpha}(Z)}$$ $$U_{X}\left(\beta^{(i)}\right)=e^{-i \beta^{(i)} \sum_{j=1}^{n} X_{j}}=\prod_{j=1}^{n} e^{-i \beta^{(i)} X_{j}}$$
状態$|β,γ⟩$やこれらの演算子の意味を説明するには量子アニーリングの知識が必要になる。とりあえず、QAOAを使うだけならこういうものだと受け入れて使ってしまえば良い。(なお、$C(Z)$というのはビット列を引数にとる関数$C(z)$の入力にパウリ演算子$Z_1⋯Z_n$を代入したものであることに注意。)
そして、$F(β,γ)=⟨γ,β|C(Z)|γ,β⟩$ を最小にするような$β,γ$を探索することで、元々の最適化問題の答えを探そうとするのが、QAOAアルゴリズムである。
QAOAアルゴリズムの手順
1.量子コンピュータ上で重ね合わせ状態$|s⟩=|+⟩⊗n$を作る。
2.パラメータ$β,γ$に応じて、量子状態に$U_C(γ^{(i)}),U_X(β^{(i)})$をかけていき、状態$|β,γ⟩$を得る。
3.量子コンピュータを用いて $⟨β,γ|C(Z)|β,γ⟩$ を測定する。
4.古典コンピュータで、$⟨β,γ|C(Z)|β,γ⟩$ がより小さくなるようにパラメータ $β,γ$ をアップデートする。
1〜4を繰り返し、最適な $β^∗,γ^∗$ を得る。
状態 $|β^∗,γ^∗⟩$に対して、$z$方向の射影測定を複数回実行し、得られた(良さそうな)測定結果 $z_1⋯z_n$ を元々の最適化問題の解として採用する。(注:測定結果 $z_1⋯z_n$ は古典ビット)
上の3つの説明をみると、QAOAは、どのようなアルゴリズムであるか、おぼろげながらに見えてきます。
量子断熱計算
最初のハミルトニアンを、$\hat{H}_{\text {start }}$として、求めたいハミルトニアンを、$\hat{H}_{\text {final }}$とすると、
$$
\hat{H}(t)=\left(1-\frac{t}{T}\right) \hat{H}{\text {start }}+\frac{t}{T} \hat{H}{\text {final }}
$$
状態ベクトル$|\Psi(t=0)\rangle$ を、$\hat{H}_{\text {start }}$の固有状態から開始して、時間発展という計算をゆっくり、行えば、$|\Psi(t)\rangle$は、$\hat{H}(t)$に追随し、最終的には、状態ベクトルは求めたい問題の固有状態を表すことになります。
ハミルトニアンに時間変化がないときは、$|\Psi(t)\rangle=e^{i \hat{H} t}|\Psi(0)\rangle$ と書けます。微小時間ごとに、$\delta_t$、順次計算していくことができます。
$
|\Psi(\delta t)\rangle=e^{i \frac{\delta t}{T} \hat{H}_{\text {start }} \delta t}|\Psi(0)\rangle
$
$
|\Psi(2 \delta t)\rangle=e^{i\left(1-\frac{2 \delta t}{T}\right) \hat{H}_{start} \delta t}|\Psi(\delta t)\rangle
$
$
|\Psi(3 \delta t)\rangle=e^{i \frac{2 \delta t}{T} \hat{H}_{\text {start}} \delta t}|\Psi(2 \delta t)\rangle
$
これは、量子アニーリングで「ゆっくりと量子項の係数を小さくしていく。このプロセスにより、容易に実現できる初期状態から出発して、自然な時間変化を経て、最適解を高い確率で実現することを目指す。」と言われているのと同様の考えかたです。アニーリングつまり焼きなましですから、温度を上げて、徐々に冷やして望ましい状態をつくっていくと理解できます。
では、次に、Qiskit textbookの Solving combinatorial optimization problems using QAOA の例をみてみましょう。
問題の定義
5個の頂点と6個の辺を持つグラフのを2つに分割するときに、分割される辺の数の最大値を求める問題です。これは、Maxcut問題と呼ばれています。
頂点を、$V={0,1,2,3,4}$ 、辺を、 $E={(0,1),(0,2),(1,2),(3,2),(3,4),(4,2)}$とします。
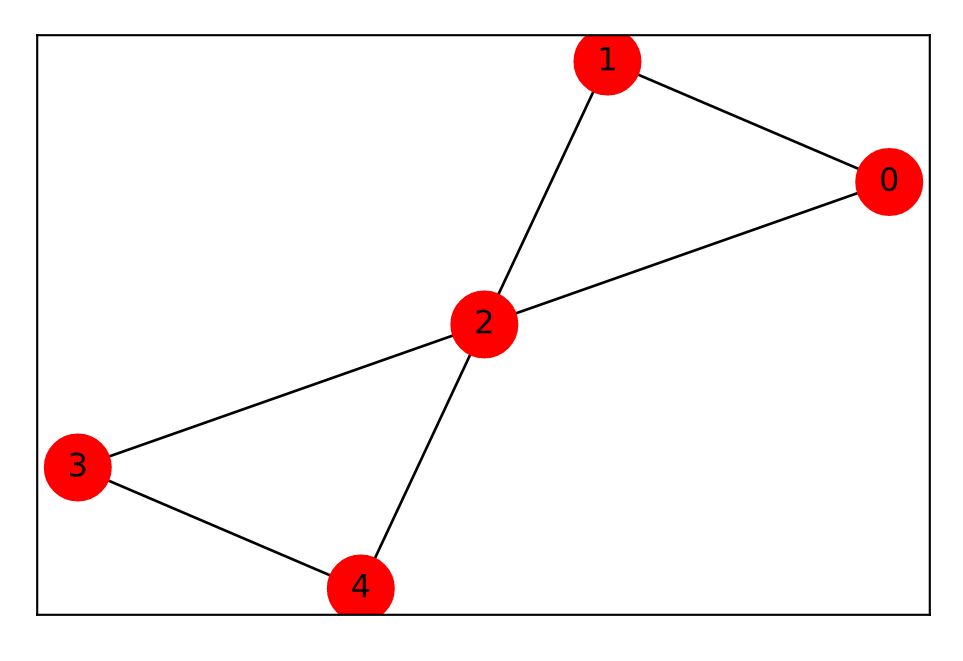
期待値は、$\left.F_{1}(\gamma, \beta)=\left\langle\psi_{1}(\gamma, \beta)\right)|H| \psi_{1}(\gamma, \beta)\right\rangle$ となります。
$$H=\sum_{(j, k) \in E} \frac{1}{2}\left(1-Z_{i} Z_{k}\right)$$
頂点を2つに分けたとき、片方のグループに属する頂点に、+1、もう一方に-1をつけるとすると、$H$は、グループ分けによって分割される辺の数に、-1をかけたものになります。したがって、Hを最小化するようなビット列$Z=Z_1,\cdots,Z_n$をみつければいいということになります。
期待値は、以下のように変形できます。
$$
f_{(i, k)}(\gamma, \beta)=\left\langle\psi_{1}(\gamma, \beta)\left|\frac{1}{2}\left(1-Z_{i} Z_{k}\right)\right| \psi_{1}(\gamma, \beta)\right\rangle
$$
この後の式の導出の詳細は、Qiskit textbook を見ていただくとして、結果として、$F_1(\gamma,\beta)$ は、以下のようになります。
$$
F_{1}(\gamma, \beta)=3-\left(\sin ^{2}(2 \beta) \sin ^{2}(2 \gamma)-\frac{1}{2} \sin (4 \beta) \sin (4 \gamma)\right)\left(1+\cos ^{2}(4 \gamma)\right)
$$
これをグラフすると以下のようになります。単純はグリッドサーチ($\gamma, \beta$を格子状で総当りする)をして、この期待値を最小化するのは、$\gamma=1.900, \beta=0.200, F_1=3.431$となります。
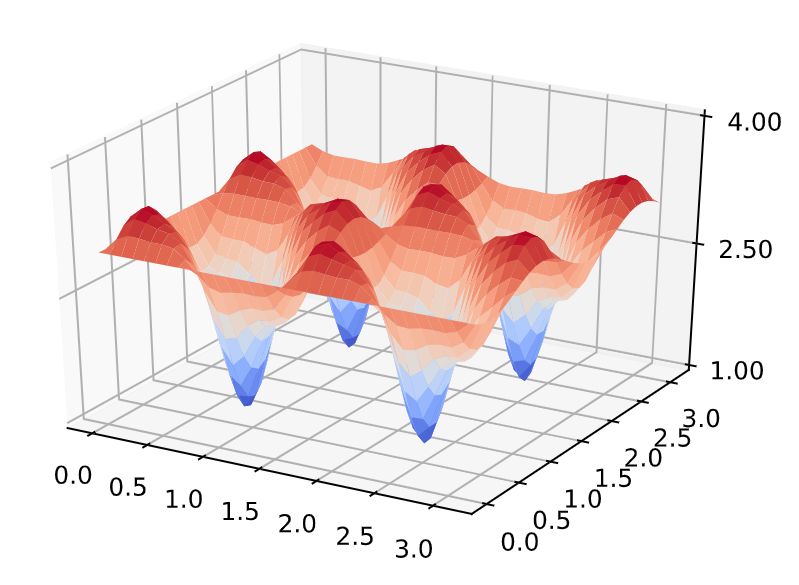
このコスト関数を見ると、最急降下法で解をもとめようとすると、複数の極小値に落ちることは容易にわかります。
量子回路
- まず、5つのアダマールゲートを準備します。
- 角度$\gamma$の6つのイジング型のゲートを各辺に設置します。
$$
U_{k, l}(\gamma)=C U 1(-2 \gamma)_{k, l} U 1(\gamma)_{k} U 1(\gamma)_{l}
$$
$$U1は、Z軸にたいする回転ゲートです。$$
$$
U 1(\lambda)=\left(\begin{array}{cc}
1 & 0 \
0 & e^{i \lambda}
\end{array}\right)
$$
$$CU1は、コントロールドU1ゲート です。$$
$$
C U 1=|0\rangle\langle 0|\otimes I+| 1\rangle\langle 1| \otimes U 1=\left(\begin{array}{cccc}
1 & 0 & 0 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 0 & 0 & e^{i \lambda}
\end{array}\right)
$$
- 角度$\beta$の$X$ 軸にたいする回転ゲート$X_{k}(\beta)=R X(2 \beta)_{k}$をおのおのの量子ビットに施します。
- 最後に測定を行うと、5ビットの結果が得られます。
- 測定から得られたビット列から、コスト関数を計算します。期待値がより小さくなるように、パラメータを調整し、これを繰り返します。
初期値から、時間発展をさせながら、ハミルトニアンを計算し、その過程でコスト関数が小さくなるようにパラメータを調整していると解釈できます。
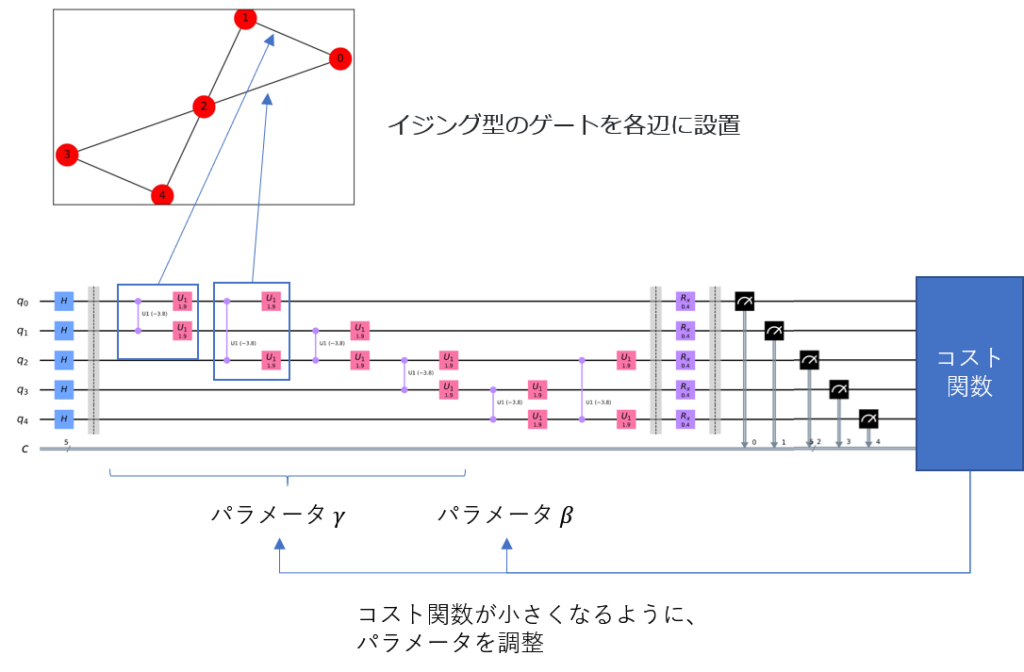
シミュレーターでの結果
シミュレーターを用いた結果です。ショット数は、10000です。
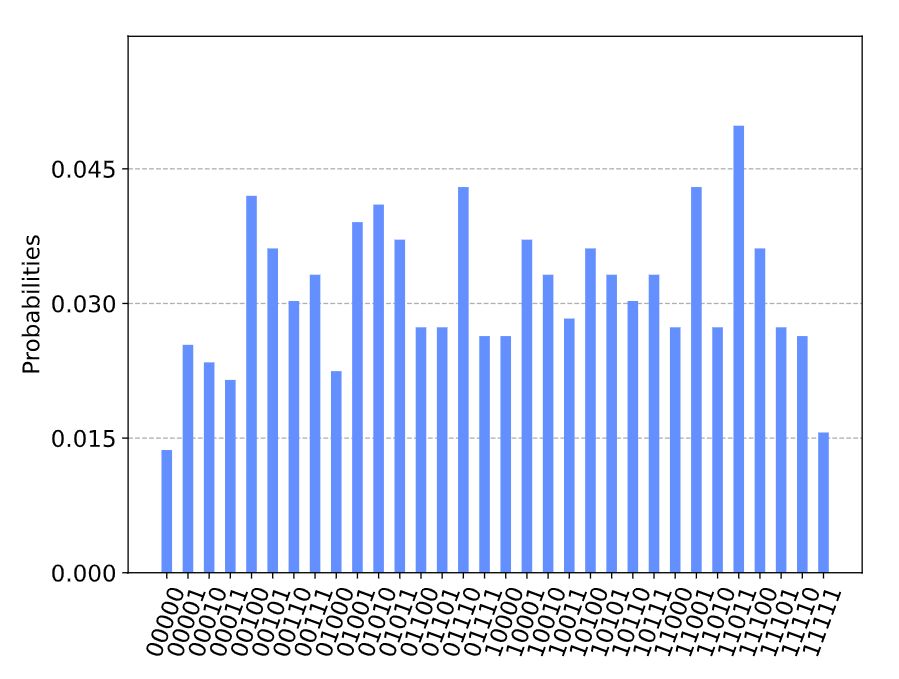
平均エネルギーを計算し、それが理論的予測と一致するかどうかを確認します。
観測されたコスト関数$C(x^∗)$の最大値と結果のビット列$x^∗$を計算します。
エネルギーのヒストグラムをプロットして、予測された平均の周りに、実際に集中しているかどうかを確認します。
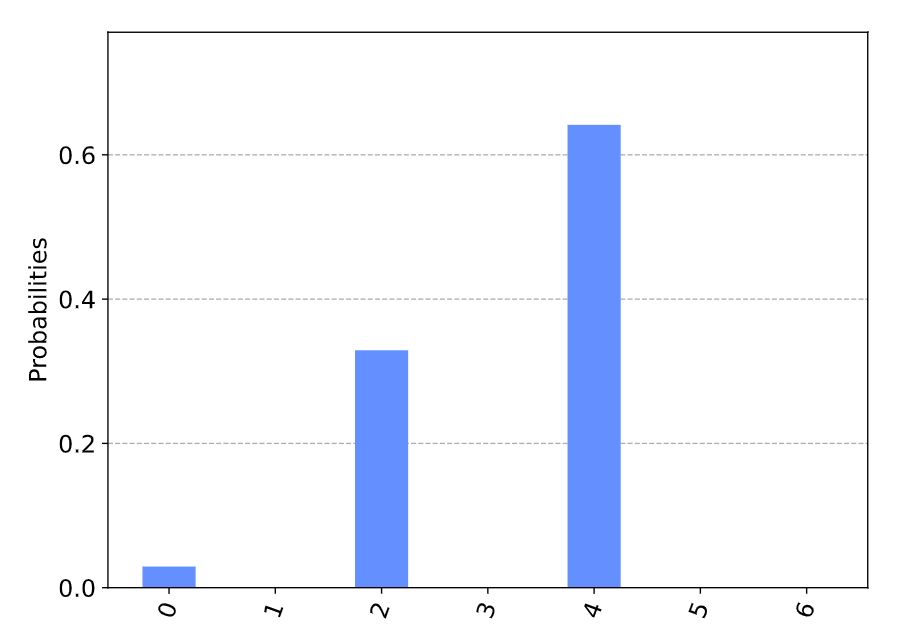
The approximate solution is x* = 10001 with C(x*) = 4
実機での結果
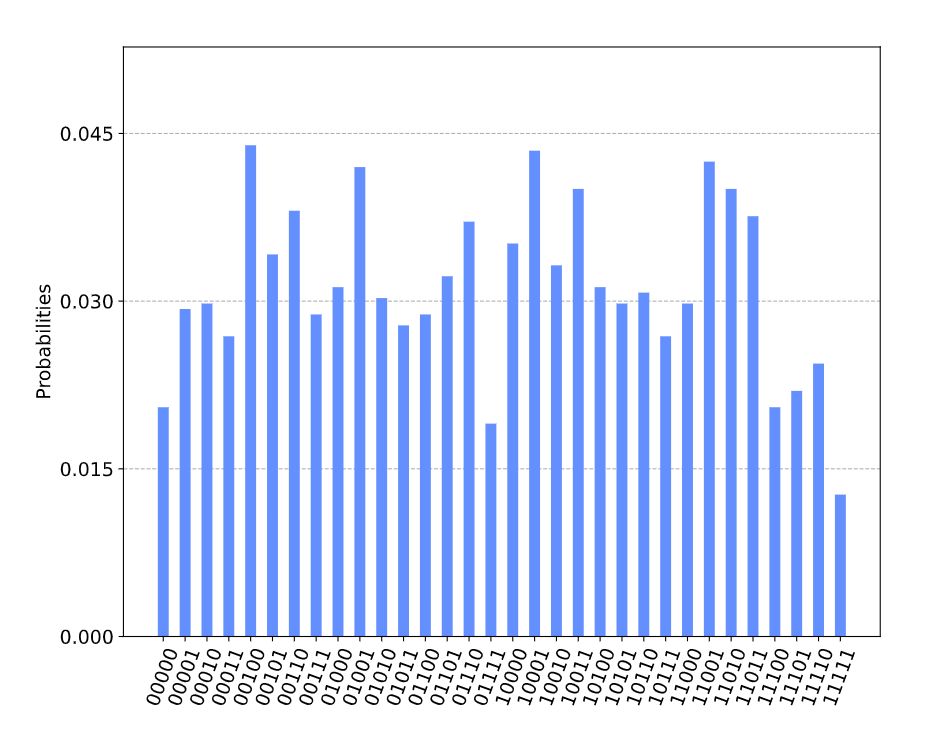
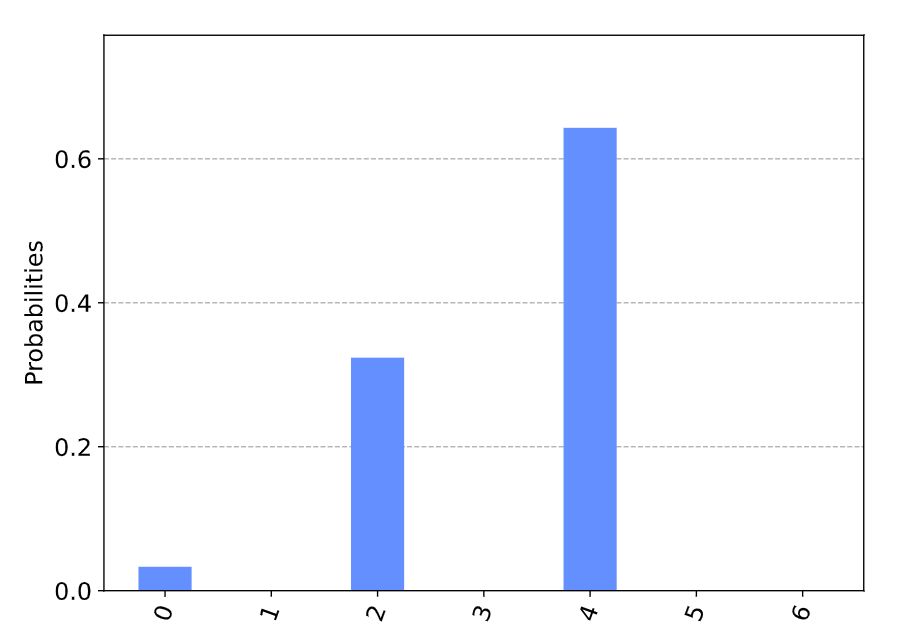
The approximate solution is x* = 10001 with C(x*) = 4
この問題をQAOAで解いたとき
このQiskit textbookの問題では、Hを最小化するようなビット列$Z=Z_1,\cdots,Z_n$をみつけることは、簡単に計算ができることは容易に想像がつきます。プログラムも作成しましたが、ここに、示すほどのものではありません。また、最大カット数が4の解も複数あります。これも、計算するまでもなく容易にわかります。QAOAで得られる結果も、その内の一つにしか過ぎません。この問題のコスト関数は、複数の極小値を持っており、QAOAで求められる解は、その内の一つというになっていると理解できます。

参考
IBM Quantum で学ぶ量子コンピュータ 湊雄一郎他著
Quantum Native Dojo (5-3. Quantum Approximate Optimazation Algorithm (QAOA): 量子近似最適化アルゴリズム)
量子アニーリングの数理
量子アニーリング 西森秀稔
Solving combinatorial optimization problems using QAOA

