量子アルゴリズム 量子位相推定(QPE)
量子位相推定(Quantum Phase Estimation、以下QPEと記す)は、量子状態の位相としての行列の固有値を求めるアルゴリズムです。行列の固有値推定は、量子化学計算など多くのアルゴリズムで使われます。
与えられたユニタリ行列 $U$に対して、$U|ψ⟩=e^{2πiθ}|ψ⟩$ となる$θ$を求めるアルゴリズムです。ここで、 $|ψ⟩$ は、固有ベクトルで、 $e^{2πiθ}$ は、固有ベクトルに対応する固有値です。
ここでは、Learn Quantum Computation using Qiskit をもとに、QPEについて、まとめてみます。
一般的なQPEの回路は、このようになります。$t$個の補助量子ビットと、状態が、$|ψ⟩$である量子ビットから構成されます。
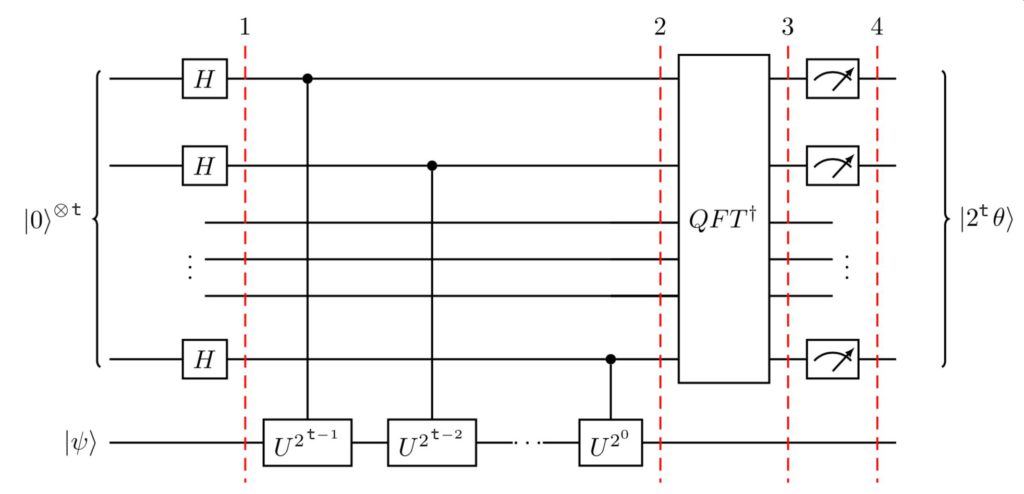
QPEアルゴリズムは、位相キックバックを呼ばれる仕組みを用いて、$U$の位相を補助量子ビットに書き込みます。そして、QFT(逆量子フーリエ変換)を施した後、計測します。
例として、$T$ゲートの場合を考えます。$T$ゲートは、状態 $|1⟩$にたいして、$e\frac{iπ}{4}$だけ位相を付け加えます。
$$
T|1\rangle=\left[\begin{array}{ll}
1 & 0 \\
0 & e^{\frac{i \pi}{4}}
\end{array}\right]\left[\begin{array}{l}
0 \\
1
\end{array}\right]=e^{\frac{i \pi}{4}}|1\rangle
$$
QPEで、以下のようになる$\theta$をもとめることができます。
$$
T|1\rangle=e^{2 i \pi \theta}|1\rangle
$$
結果として、以下のような値が得られるはずです。
$$
\theta=\frac{1}{8}
$$
この例では、3個のQビットをもちいて、推定ではなく正確な値を得ることができます。
量子回路は、このようになります。

この回路を、2048回(ショット)実行した結果は、以下のようになります。

結果として、(001)が得られました。10進数にすると、1になります。$\theta$を得るためには、$2^2$で割らないといけません。したがって、結果は、以下のようになります。期待どおりの正確な値が得られました。
$$
\theta=\frac{1}{2^{3}}=\frac{1}{8}
$$
これはあまりにも単純な例だったので、$T$ゲートのかわりに、$\theta=\frac{1}{3}$のゲートを使ってみます。量子回路は、上と同じものを使います。
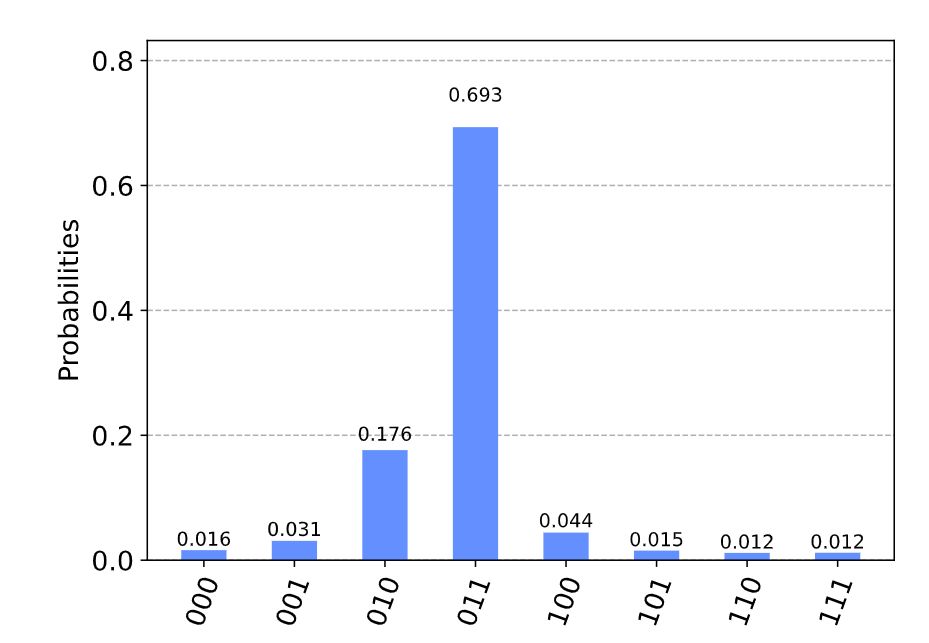
結果は、$\theta=0.3333 \ldots$となるはずですが、最も確からしい結果として、010(10進数で2)$\theta=0.25$ と、011(10進数)で3、$\theta=0.375$が得られました。正しい値は、この間で、不正確です。
もっと正確にするには、補助量子ビットの数を増やさないといけません。補助量子ビットの数を5個にしてみます。


最も確からしい結果は、01011(10進数11)と01010(10進数10)で、$\theta$は、以下のようになります。
$$\theta=\frac{11}{2^{5}}=0.344$, or $\quad \theta=\frac{10}{2^{5}}=0.313$$
ここまでは、シミュレーターを使った結果でした。では、実機を使えばどようになるのでしょうか。

シミュレーターを用いた結果と同様の結果が得られましたが、実機ではノイズとエラーのために001以外の結果もでてきています。
参考文献

