
量子コンピュータの原理
作成: 2022/09/25
目次
量子コンピュータの原理量子力学と量子コンピュータ、量子ビットハミルトニアンとエネルギー量子コンピュータの動作原理古典ビットと量子ビットの違い1量子ビット測定2量子ビット2つの1量子ビットエンタングルメント(量子もつれ)状態ベクトルを視覚化するブロッホ球量子ゲート1量子ビットゲートパウリゲートアダマールゲートS, Tゲート位相ゲート回転ゲート2量子ビットゲート基底ベクトル表記の順番CNOTゲート制御ユニタリゲート制御Zゲート制御アダマールゲートSWAPゲート主な量子ゲートまとめ量子コンピュータはどのように計算をするのか量子ビットの操作は具体的にどうするのかゲート操作の例量子コンピュータは万能量子コンピュータの制約事項・課題量子コンピュータの現在量子アルゴリズムの種類FTQCアルゴリズムNISQアルゴリズムPython と IBM Quantum, Qiskit でプログラミングIBM Quantum実行環境IBM Quantumのアカウント作成IBM Quantum ローカル実行環境Anacondaのインストールと環境設定Qiskit フレームワークの全体像TerraAerIgnisAquaQiskit とPython を用いた量子コンピュータのプログラミングQiskitのプログラムの基本的なステッププログラミングの実例ステップ 1 : パッケージをインポートする。ステップ 2 : 量子回路を定義する。ステップ 3 : ゲートを追加する。ステップ 4: 回路を可視化するステップ 5: 演算のシミュレーションステップ6: 演算結果の可視化実機で実行汎用量子計算量子フーリエ変換(Quantum Fourier Transform, QFT)量子位相推定(Quantum Phase Estimation, QPE)Shorのアルゴリズム量子古典ハイブリッドアルゴリズム量子古典ハイブリッドアルゴリズムの基本ハミルトニアンと期待値量子変分アルゴリズム VQEQiskit プログラム例QAOAQiskit プログラム例 MaxcutQiskitを用いてVQE,QAOA で実問題を解くポートフォリオ最適化四銘柄のポートフォリオ最適化問題ライブラリのインポート時系列データ(金融データ)の生成期待リターンと共分散行列の計算Qiskit Finance のポートフォリオ最適化クラスMinimum Eigen Optimizer(最小固有値オプティマイザー)古典コンピュータの最適化アルゴリズムで問題を解くVQEを使ったソリューションQAOAを使ったソリューションナップザック問題一般的なナップサック問題をQAOAで解く動的計画法(古典コンピュータによる計算)QAOAによる解法蓄電池システムの収益最大化問題設定電池による収益の最適化をQAOAで解く量子機械学習量子古典ハイブリッド機械学習1. 入力データの量子状態へのエンコーディング2. 学習用量子回路3. 損失関数4.回路パラメータ更新量子機械学習の実例パッケージのインポートQiskitを用いた量子回路を作成しますPyTorchを用いた量子古典回路の作成データの準備ハイブリッド・ニューラルネットワークの作成ネットワークの学習学習曲線を表示しますテストを行います。推論結果を表示しますサンプルプログラムについて参考文献
量子力学と量子コンピュータ、量子ビット
量子というのは、粒子と波の両方の性質を両方もつ原子、電子、中性子、陽子、光を粒子とみんなした光子などが量子の代表的なものです。量子力学的な現象を用いているわけですから、量子力学とは切っても切れない関係にあるわけです。ここでは、まず、量子コンピュータで様々な問題を解く際に押さえておくべき基本的な概念をみてみます。
量子の振る舞いは、次のシュレディンガーの波動方程式を解くことによってもとまります。
この式の両辺はエネルギーであって、粒子が持つエネルギーは、波動関数にハミルトニアンという運動エレルギーと位置エネルギーの和からなる演算子
波動関数に作用する演算子であるハミルトニアンの固有値と固有関数を求めれば、波動関数が解け、量子力学的な状態がわかります。ハミルニアンという名称は、1830年代に活躍したウィリアム・ローワン・ハミルトンにちなんでいます。ハミルトニアンを、波動関数に作用させるとエネルギーが計算できます。ハミルトニアンは行列ですから、エネルギー変換行列とでも呼んだほうが分かりやすいかも知れません。
ハミルトニアンの固有値と固有関数を求め、最低エネルギー状態とそれより一つエレルギーが高い状態が求まったとします。
2つの状態だけを考えて、量子状態は、この2つの状態に対応する波を重ね合わせたものとして記述できます。複素数
ハミルトニアンとエネルギー
量子状態にハミルトニアンをかけるとエネルギーになるということは重要です。たとえば、量子古典ハイブリッドアルゴリズム(NISQアルゴリズム)で解くことの出来る問題の典型は、問題がハミルトニアン、つまり状態をエネルギーに変換する行列が与えられ、安定なエネルギー状態を求めることに置き換えることができます。つまり、固有値と固有ベクトルを求めることになります。または、言い換えると安定なエネルギー状態のうち、一番エネルギーが小さいものを求めるということになります。
量子コンピュータの動作原理
量子コンピュータは、「重ね合わせ」や「量子もつれ」と言った量子力学的な現象を用いて従来のコンピュータでは現実的な時間や規模で解けなかった問題を解くことが期待されるコンピュータです。量子コンピュータの世界では、従来のコンピュータは、量子力学的な現象に基づいていないという意味で、古典コンピュータと呼ばれます。
量子コンピュータは、量子力学的な重ね合わせによって、
古典ビットと量子ビットの違い
図1にしめすように、古典コンピュータでは、ビットは、0と1かのどちらか値をとります。量子ビットでは、基底ベクトル |0⟩ |1⟩ に係数を掛けて足し合わせた状態ベクトル
図1 古典ビットと量子ビット
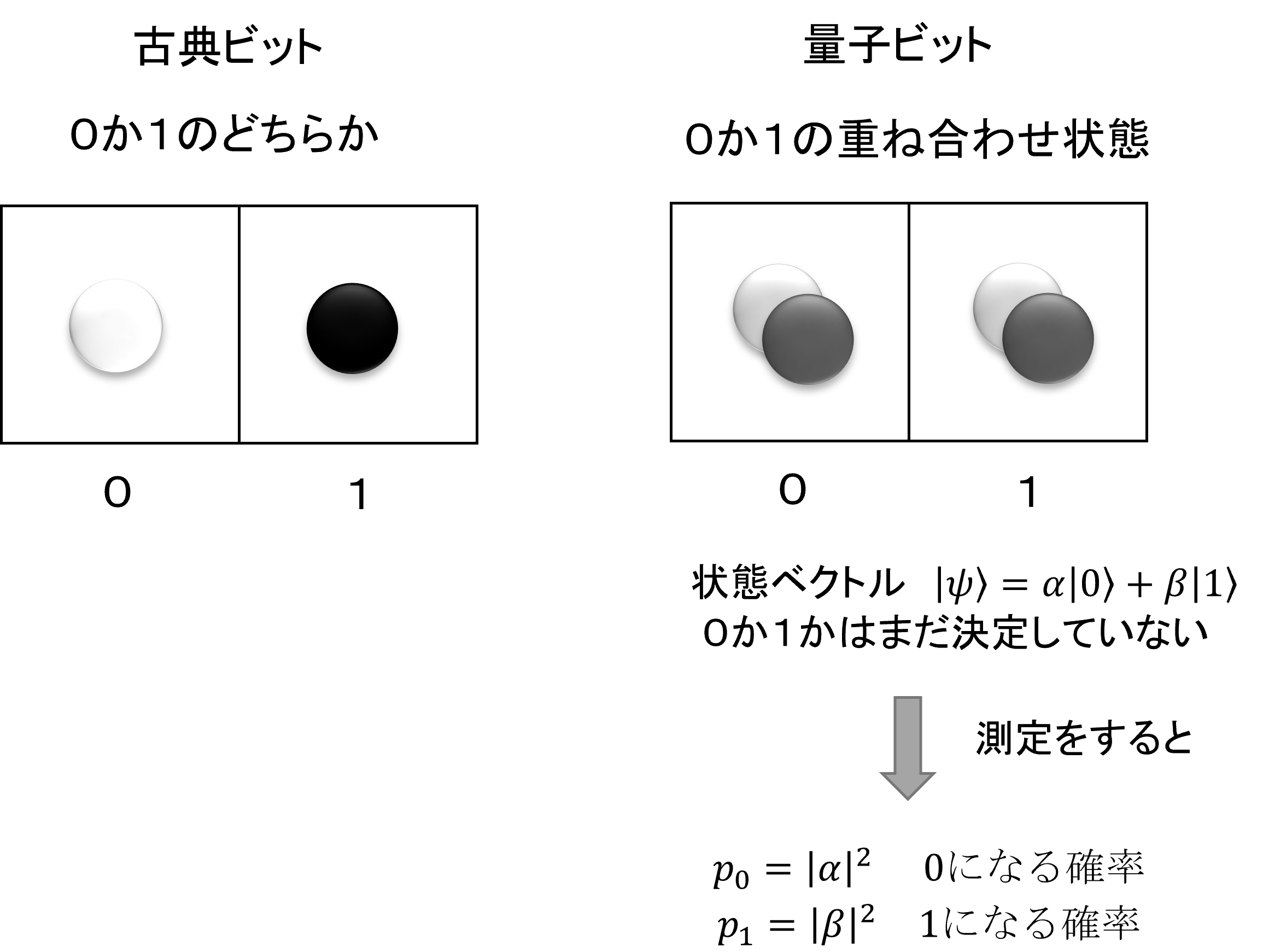
1量子ビット
式(1)、(2)で示すように、一つの量子ビットは、2つの基底ベクトル、
これは状態ベクトルや量子ビットと呼ばれます。式(3)でしめす足し合わせた状態のことを重ね合わせ状態と呼びます。
測定
残念ながら、量子力学では、この複素確率振幅は、直接知ることができません。測定という操作をしたときに、0か1かが確率的に決まります。また、測定を行うと、状態ベクトルは、測定結果が
状態ベクトル
このような表現の方法は、ディラック記法と呼ばれ、
2量子ビット
2個の量子ビットの状態ベクトル
ここでも、状態ベクトルの絶対値が量子の存在確率を表しますので、
1量子ビットの場合と同様、
2つの1量子ビット
2 のの1量子ビット
基底ベクトル
つまり、上の2量子ビットの基底ベクトル
エンタングルメント(量子もつれ)
重ね合わせ状態に加えて、重要な量子ビット間の関係に、エンタングルメント(量子もつれ)があります。2つの1量子ビットが、上のテンソル積で記述できない状態が存在します。例えば、式(13)のような状態です。この状態のことをエンタングルメント(量子もつれ)といい、量子コンピュータにおいては、非常に重要な役割を果たします。
量子もつれとは、複数の量子ビットがつくられるときや、相互作用するとき、空間的に近接した場合に起こる物理現象です。量子ビットが大きく離れている場合も含めて、量子ビットの量子状態が他の量子ビットの状態に依存するという不思議な現象です。
状態ベクトルを視覚化するブロッホ球
量子ビットを単位球面上の点として視覚化するのが、Bloch(ブロッホ)球です。状態ベクトル
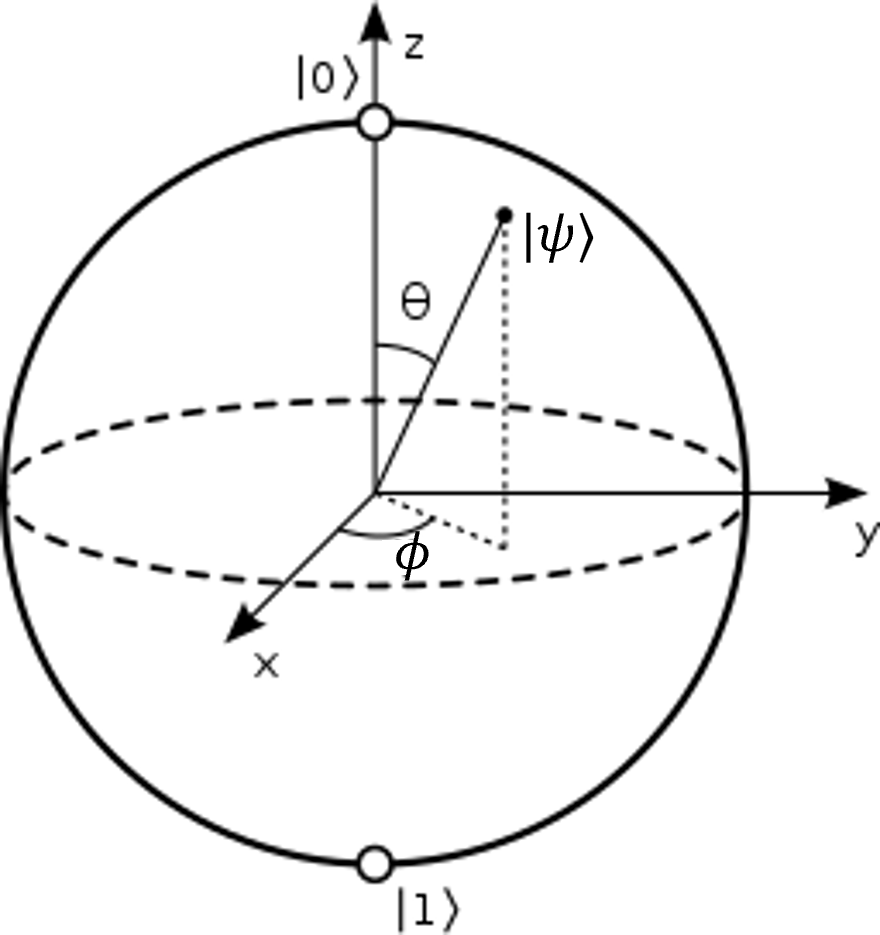
図2 ブロッホ球
量子ゲート
古典コンピュータでは、論理ゲートは、AND, OR, NOTなどですが、量子コンピュータでは、量子ビットの回転操作を行う量子ゲートによって、計算が行われます。量子ゲートの回転操作は行列によて表わされます。式(15)のように、状態ベクトル
この行列
1量子ビットゲート
1量子ビットゲートには、パウリゲート、アダマールゲート、Sゲート、Tゲート、位相ゲート、回転ゲートなどがあります。
パウリゲート
ブロッホ球のX軸、Y軸、Z軸で、180°回転させるゲートで、Xゲート、Yゲート、Zゲートと呼ばれます。
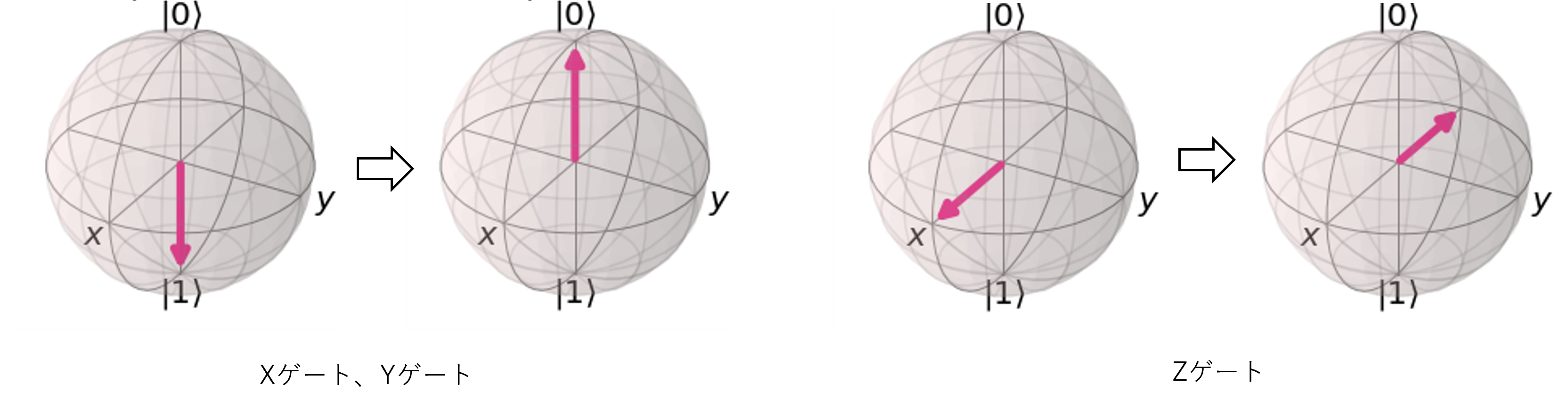
図3 Xゲート、Yゲート、Zゲート
アダマールゲート
Z軸とX軸にたいして45度傾く軸で180°させるゲートで、Hゲートと呼ばれます。アダマールゲートを使うことにより、量子ビット
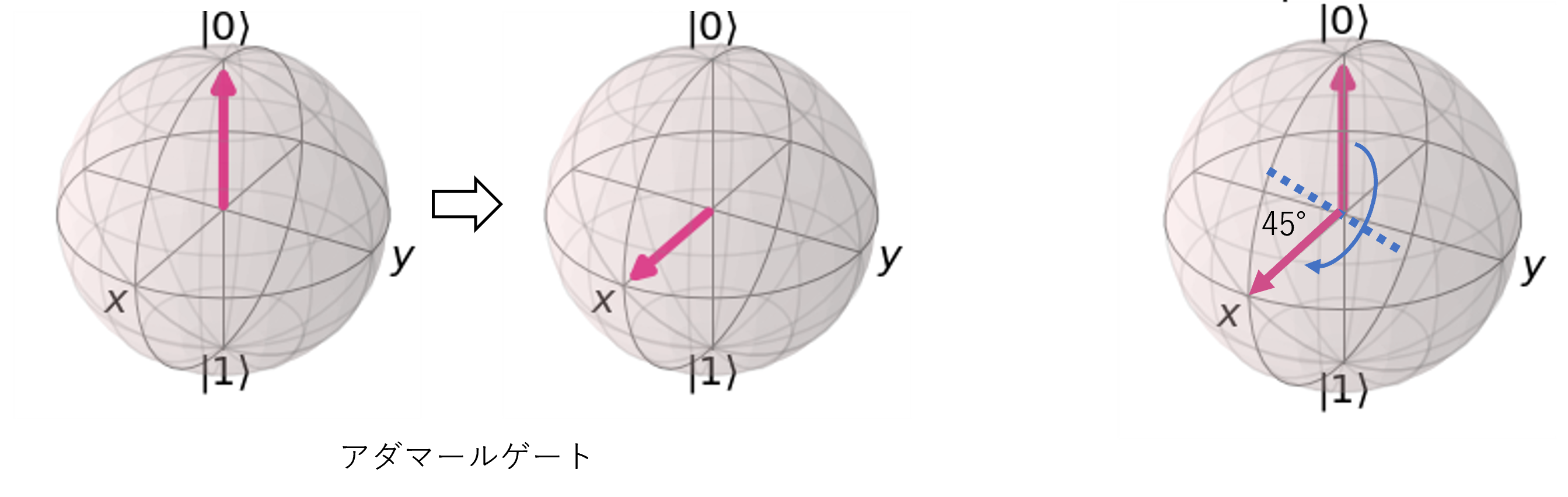
図4 アダマールゲート
S, Tゲート
位相を回転させるゲートです。
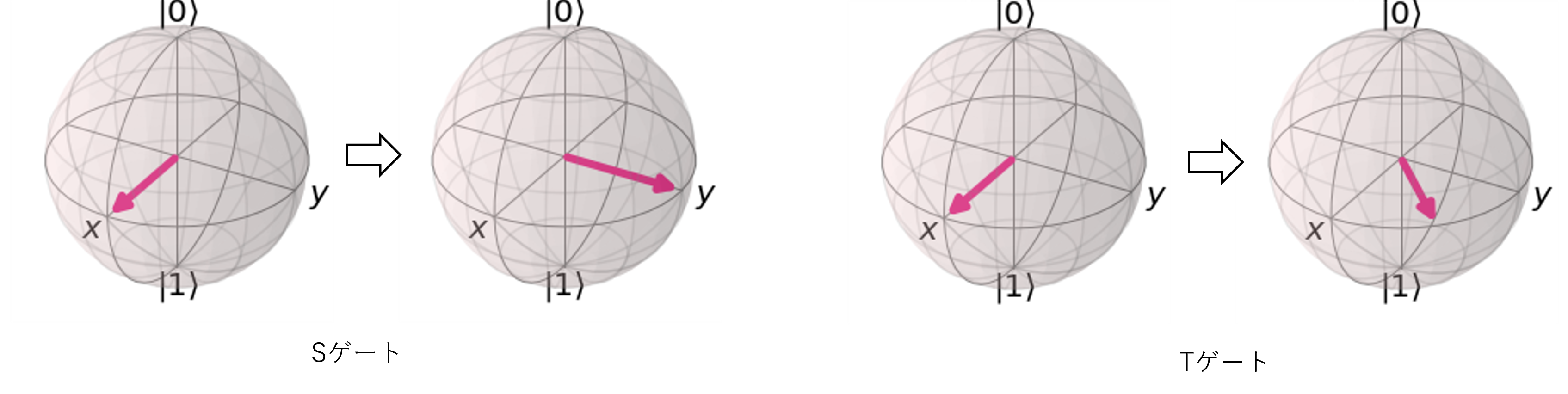
図5 sゲート、Tゲート
位相ゲート
量子ビットを任意の位相だけ回転させるゲートです。
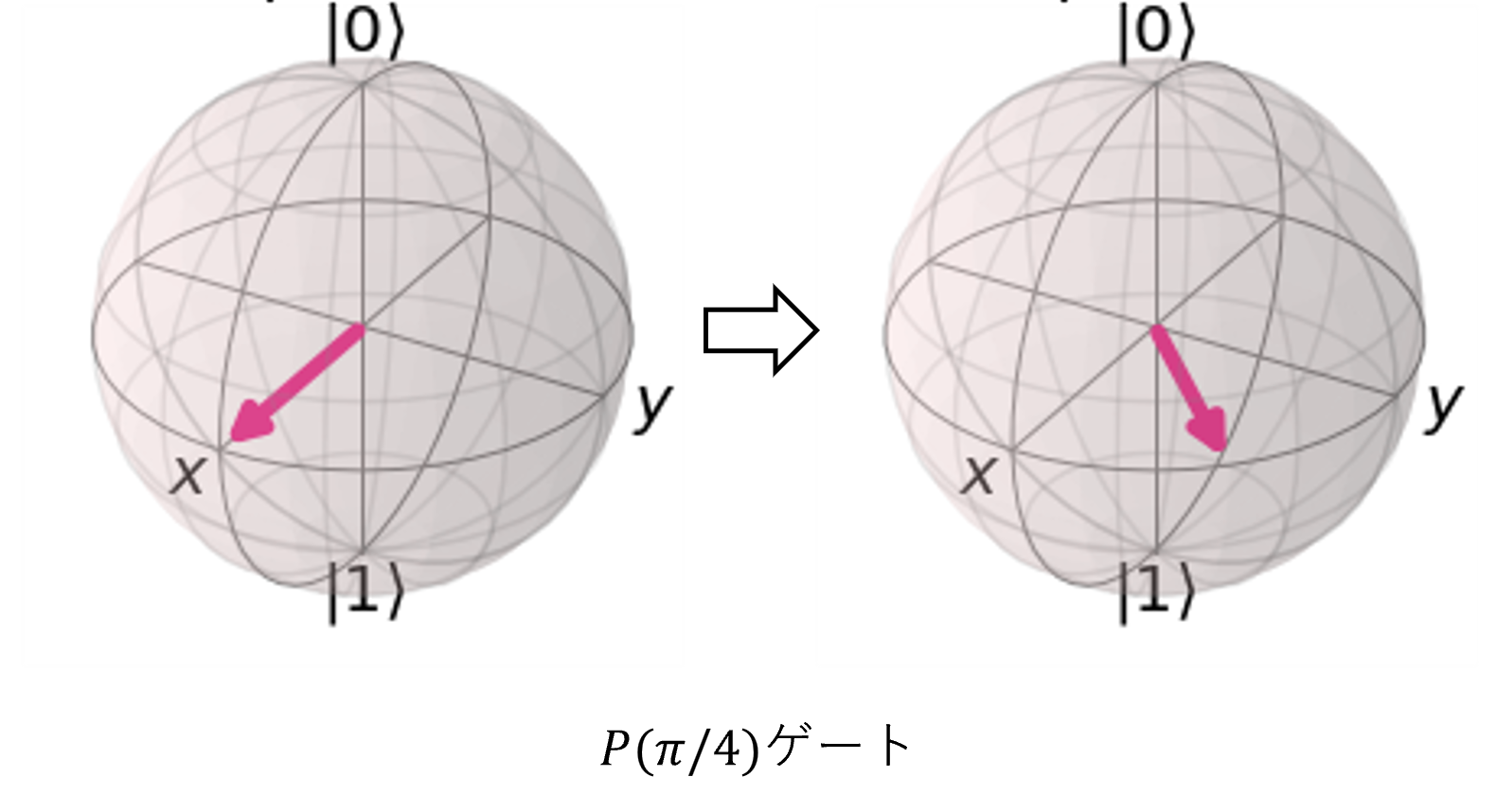
図6 位相ゲート
回転ゲート
各軸にたいして量子ビットを回転させるゲートです。
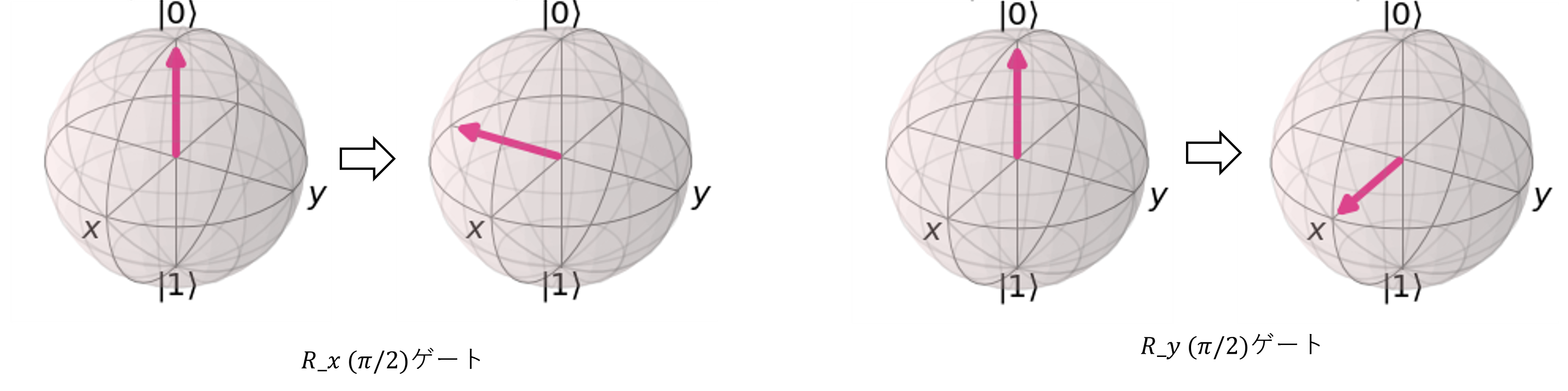
図7 回転ゲート
2量子ビットゲート
2量子ビットゲートには、CNOTゲート、制御ユニタリゲート、SWAPゲートなどがあります。SWAPゲートを除く、2量子ビットゲートは制御タイプです。制御2量子ビットゲートは 最初の量子ビットが |1⟩ の時に、2番目の量子ビットに対して単独の量子ビットゲートを適用します。このとき最初の量子ビットを制御量子ビットと呼び、2番目の量子ビットをターゲット量子ビットと呼びます。
基底ベクトル表記の順番
通常、状態をケットであらわすときに、「1番目」の量子ビット、「2番目」の量子ビットの状態に対応する0と1を左から順番に並べて表記されます。例えば、最初の qubit が |0⟩ 状態で、2番目のものが |1⟩ 状態の場合、その結合状態は |01⟩ です。ところが、今回、プログラミングにもちいるQiskit では、古典コンピューター上でのビット列表現と同じ順序同様にし、測定が実行された後のビット文字列から整数への変換を容易にするという理由から、 最上位ビット (Most Significant Bit - MSB) を左にとり、最下位ビット (Least Significant Bit - LSB) が右にとられます。つまり、「1番目」の量子ビット、「2番目」の量子ビットの状態に対応する0と1を右から順番に並べて表記されます。上の例でいえば、最初の qubit が |0⟩ 状態で、2番目のものが |1⟩ 状態の場合、その結合状態は |10⟩ となります。この点は、注意が必要です。 今回は、Qiskitをもちいたプログラミングを紹介しますので、以下では、Qiskitの基底ベクトル表記を用います。
CNOTゲート
制御Xゲートとも呼ばれます。制御量子ビットが、cx(q[1],q[0])。
LSBを制御にした場合は、以下のようになります。Qiskitではcx(q[0],q[1])。
制御ユニタリゲート
CNOTでは、ターゲット量子ビットに、Xゲートを作用させましたが、その他の量子ゲート
制御Zゲート
制御量子ビットが |1⟩ である場合には、Z ゲートがターゲット量子ビットの位相を反転させます。 この行列は、制御量子ビットが、MSBでも、LSBでも、同じになります。
制御アダマールゲート
制御量子ビットが |1⟩ のとき、ターゲット量子ビットに H ゲートを作用させます。制御がLSB量子ビットの時は、以下のようになります。
SWAPゲート
SWAPゲートは2量子ビットの値を交換します。
主な量子ゲートまとめ
| ゲート | 回路 | 行列 |
|---|---|---|
| パウリXゲート | 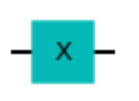 | |
| パウリZゲート | 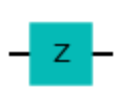 | |
| アダマールゲート | 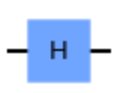 | |
| Tゲート | 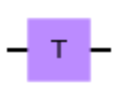 | |
| CNOTゲート |  |
図8 主な量子ゲートのまとめ
量子コンピュータはどのように計算をするのか
これまで、量子ビットとはなにか、量子ゲートにはどのようなものがあるかを見てきました。では、量子コンピュータは、量子ビット、量子ゲートを用いて、どのように計算をするのでしょうか。
量子コンピュータでは、まず、すべての状態の重ね合わせを準備します。この状態に、量子ビット間を干渉させるための操作つまり量子ゲートによる操作を順次施します。状態ベクトルつまり量子ビットは、波の性格をもつため干渉するというのがポイントです。量子ビットの間の干渉の結果を測定することによって計算が行われます。複数の量子ビットの状態を同時に操作できるのも量子コンピュータの大きな特徴の一つです。
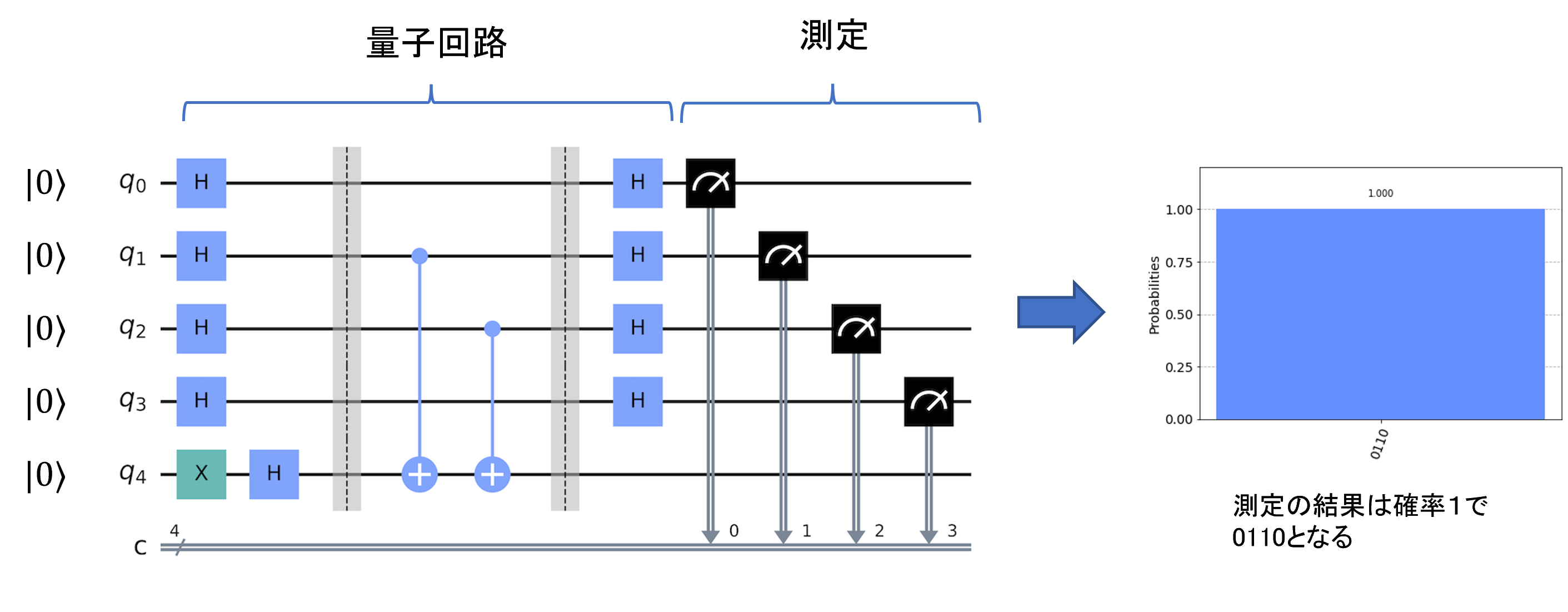
図9 量子コンピュータの基本
量子ビットの操作は具体的にどうするのか
これまで、量子ビットや量子ゲートを、ベクトルや行列で説明してきましたが、量子コンピュータでは、具体的に、どのように量子ビットを操作しているのかでしょうか。代表的な量子ビットである超電導量子ビットの場合で、見てみたいとおもいます。
超電導量子ビットは、図10に示すように、2つの超電導電極を薄い絶縁膜でつないだものです。
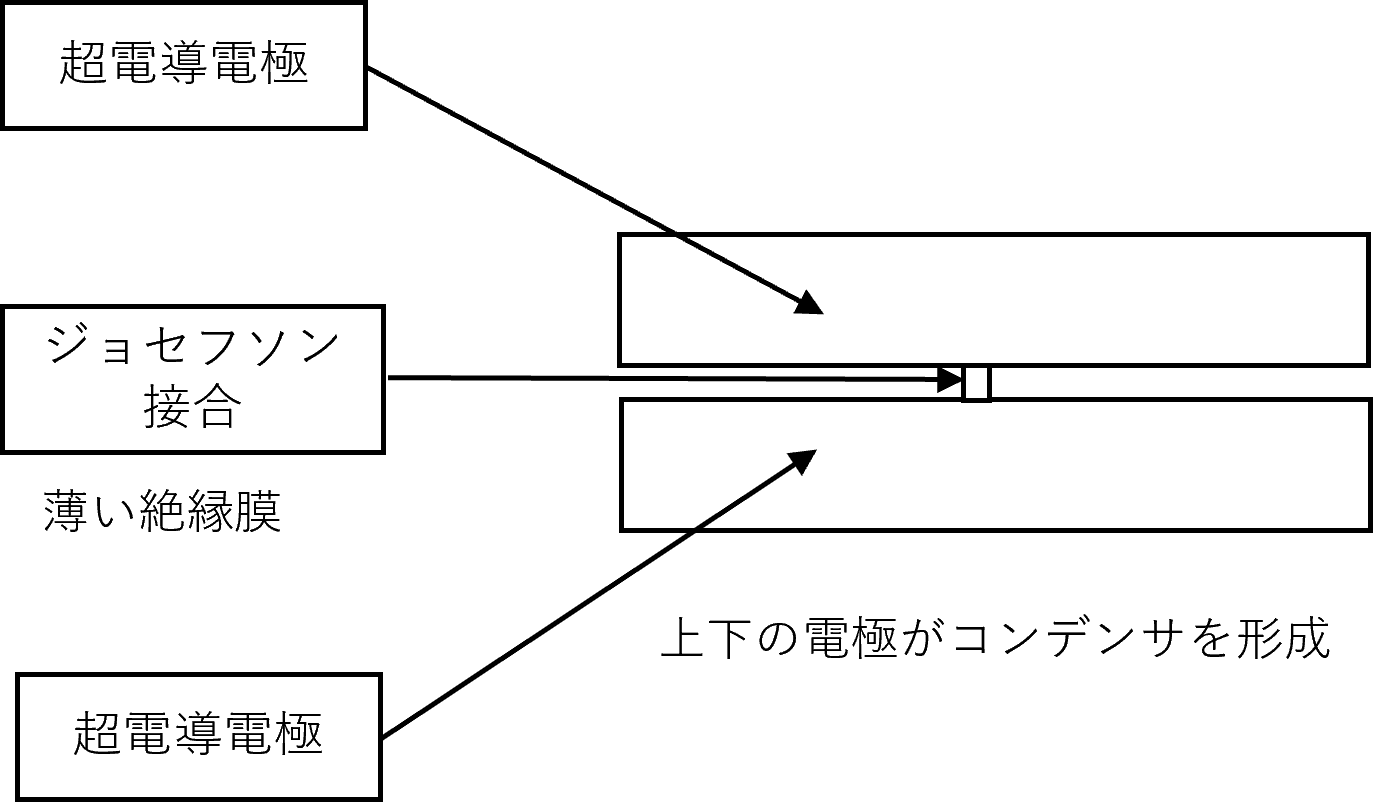
図10 超電導量子ビットの構造
これは、非線形インダクタとコンデンサによるLC共振回路とみなせます。量子状態
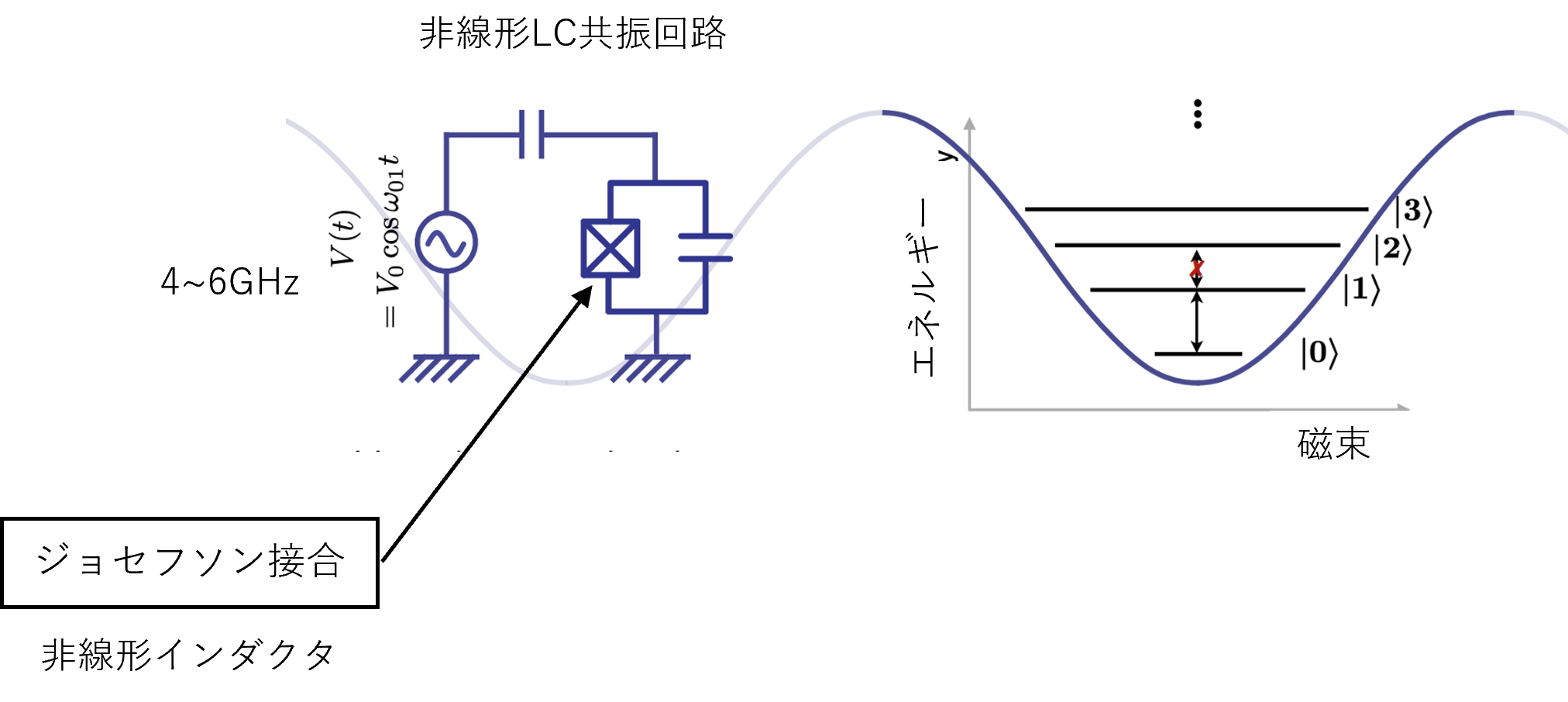
図11 超電導量子ビットの操作 (12)
重ね合わせ状態をつくるには、
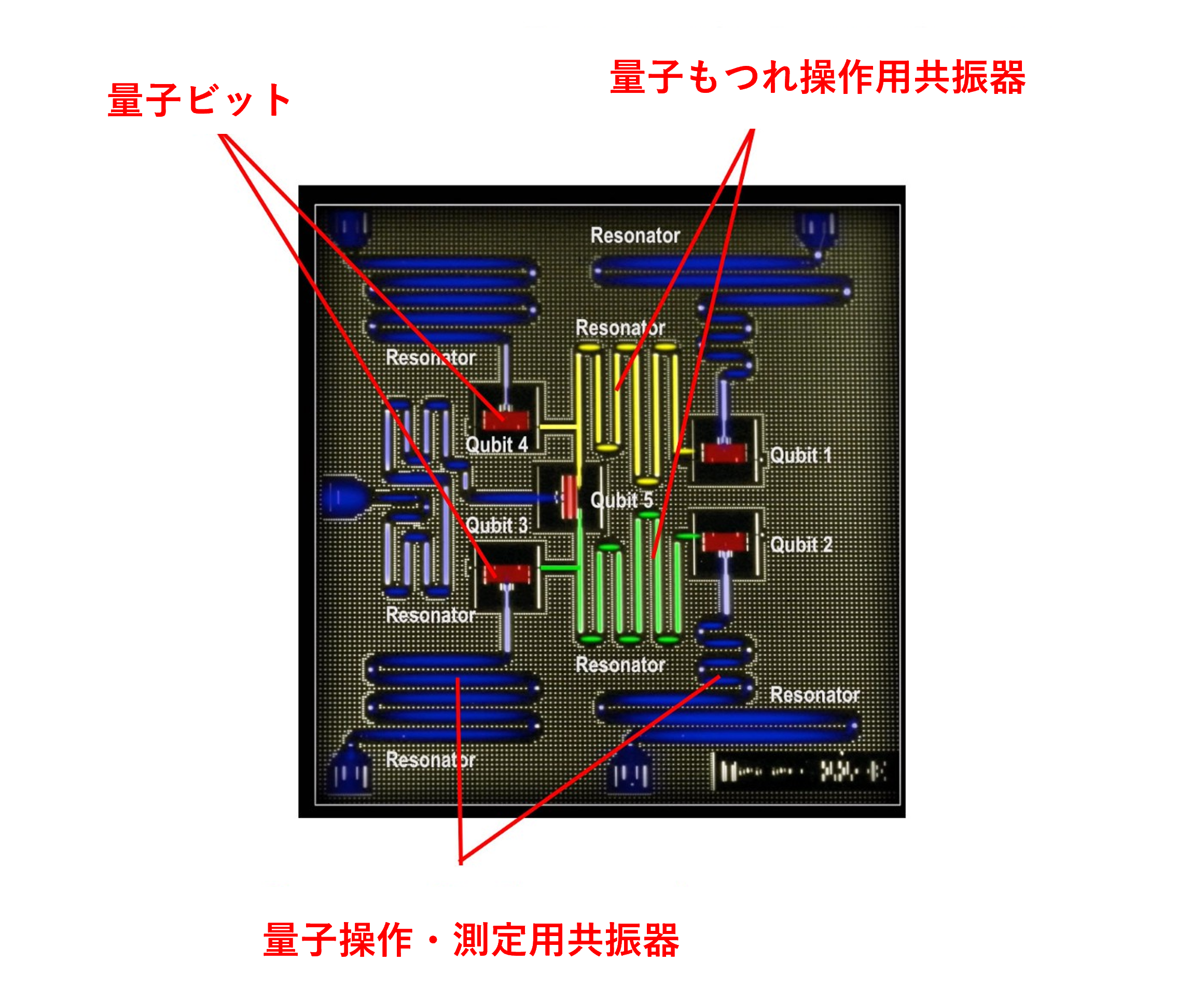
図12 超電導量子チップの構造 (13)
出所: https://www.ibm.com/blogs/research/2017/11/qubit-explained/
ゲート操作の例
図13の上の縦軸は電磁波の強度を表しています。実線が1量子ビットの操作で、破線が2量子ビットの操作です。まず、初期状態を準備し、量子回路を通した後、計測を行います。このように、マイクロ波や交流パルスを、順次、印加することによって、量子ビットを操作し、計算を行っていきます。図13の下に対応するゲートからなる量子回路をしめしています。
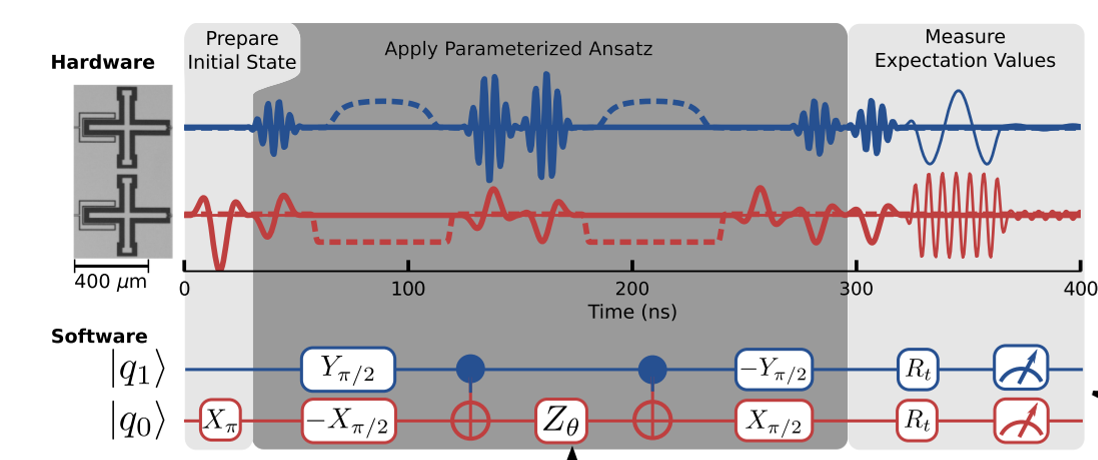
図13 量子ビットゲート操作の例 (14)
出所: https://journals.aps.org/prx/pdf/10.1103/PhysRevX.6.031007
量子コンピュータは万能
古典コンピュータが、NANDゲートをくみあわせれば任意の計算が可能なように、CNOT、アダマールゲート、Tゲートがあれば任意の計算が可能なことがわかっています。ただし、ノイズの影響により正しい計算ができるかどうか、その計算が早いかどうかは別問題だということに注意が必要です。
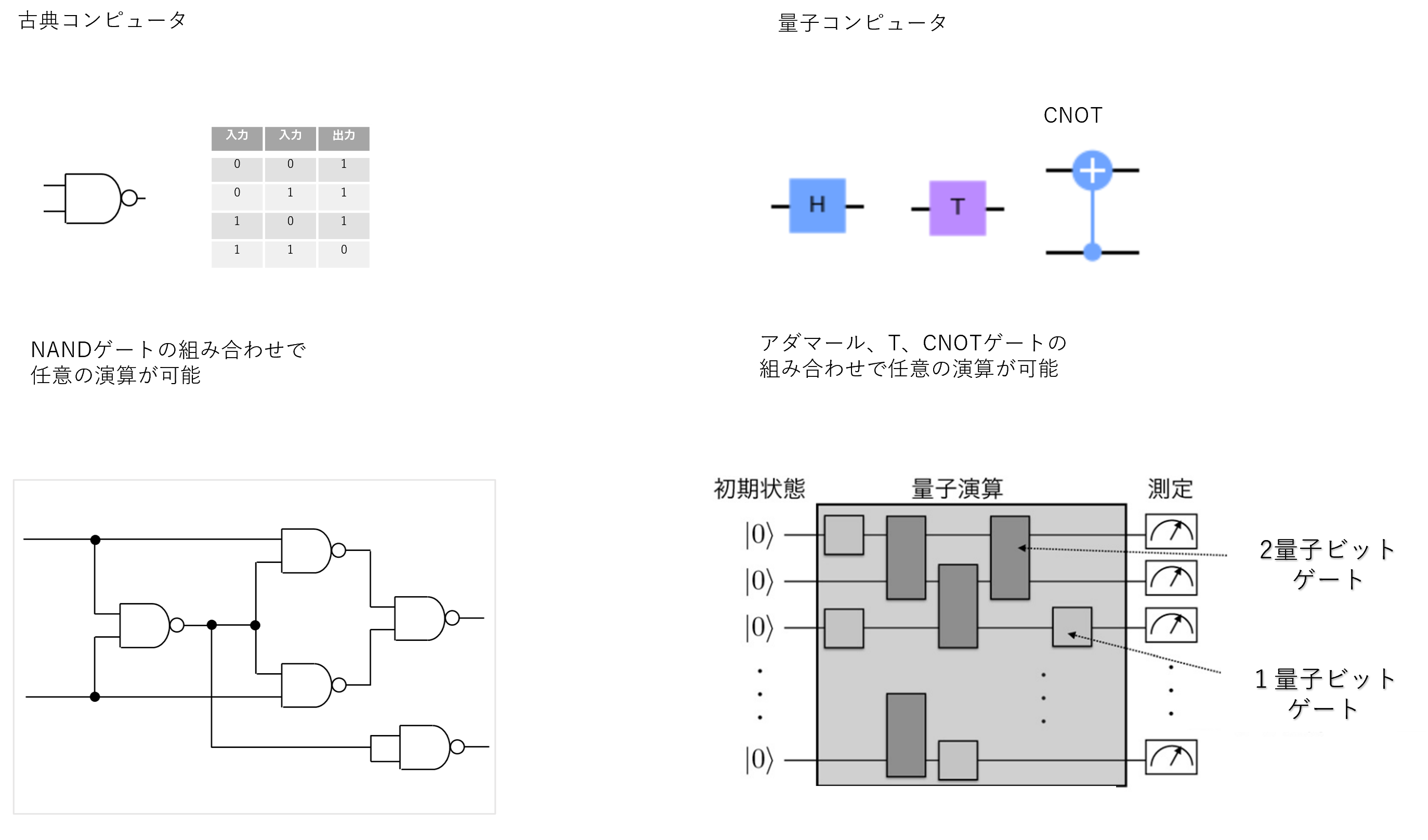
図14 古典コンピュータと量子コンピュータ
量子コンピュータの制約事項・課題
理想的な量子コンピュータは万能であり、古典コンピュータを凌ぐ能力があることはわかっています。ただし、まだまだ、多くの制約事項や課題をかかえています。
- コヒーレンス時間 量子ビットの状態は、古典ビットと比べると、ノイズに弱く、変化してしまいやすいものです。|1⟩という状態にしたはずの量子ビットが、時間が経つと |0⟩ という状態になってしまいます。それにくわえて|0⟩、|1⟩ の重ね合わせ状態がくずれてしまうことも起こります。一定時間経つと、量子ビットの重ね合わせの状態は全てくずれてしまいます。こような量子性が保たれる間の時間をコヒーレンス時間といいます。コヒーレンス時間内に計算を終えないといけません。
- エラー 古典コンピュータにおいても、メモリなどでビットエラーが生じるように、量子コンピュータでも、温度、磁場のゆらぎ、隣接量子ビットの動作などのノイズの影響を受けて、ゲート操作時や測定時にエラーが起こることがあります。
このように、現時点のハードウェアでは、演算中に発生するエラーで正しい計算を行うことが困難なことに加えて、コヒーレンス時間の制約から、深い量子回路の計算も困難です。誤り訂正ありの量子コンピュータが実現されて初めて、実用的な計算を行うことができると言われています。
量子コンピュータの現在
誤り訂正ありの量子コンピュータの実現は、まだまだ先のことです。現在実現されているハードウェアは、エラーの原因となるノイズがある中規模量子デバイス、Noisy Intermediate-Scale Quantumです。今後は、NISQと呼びます。現時点では、性能・機能に制約が多いNISQのうまい使い方の研究開発が進められていたり、誤り訂正ありの量子コンピュータの応用研究がすすめられている段階です。また、現在のNISQで解ける問題の規模は限られており、古典コンピュータで十分高速に解くことができます。
規模が大きくなると古典コンピュータで解くことが困難な問題の一つに、巡回セールスマン問題などの組み合わせ最適化問題があります。セールスマン巡回問題とは、セールスマンが所定の複数の都市を1回だけ巡回する最短経路を計算するというものです。都市数が増加すると計算量が急速に増加しますので、都市数が多くなると現実的な時間で計算が終わりません。このような問題を現実的な時間で解くことが、量子コンピュータに期待されていますが、残念ながら、現状では、量子コンピュータで扱える都市数が少ないとともに、古典コンピュータに勝る計算速度が実現されているわけではありません。今後の量子コンピュータの発展が期待されています。
量子アルゴリズムの種類
量子コンピュータでは、すべての状態の重ね合わせを準備し、順次、量子ゲートの操作を加えていき、量子ビット間の干渉を起こさせ、回答が高確率で得られるような特別なアルゴリズムが必要です。これは古典コンピュータで、様々なアルゴリズムが作られているのと同じです。量子アルゴリズムは、大きく2つに分類されます。
- FTQCアルゴリズム、long-termアルゴリズム 誤り訂正ありの量子コンピュータ(FTQC、Fault Tolerant Quantum Computer)でしか実行が困難なアルゴリズム
- NISQアルゴリズム、量子古典ハイブリッドアルゴリズム 実現しつつあるノイズありの中規模量子デバイス(NISQ,Noisy Intermediate-Scale Quantum)で実行可能なアルゴリズム 一定のエラーがある前提で、量子コンピュータと古典コンピュータを組み合わせたアルゴリズム
FTQCアルゴリズム
FTQCアルゴリズムの代表的なものには、以下のようなものがあります。
- ショア(Shor)のアルゴリズム 素因数分解を解くアルゴリズムです。
- グローバー(Grover)のアルゴリズム 非構造化データを高速に検索するアルゴリズムです。
- 量子フーリエ変換 離散フーリエ変換を行うアルゴリズムです。他の量子計算の要素として用いられることが多いアルゴリズムです。
- 量子位相推定(Quantum Phase Estimation, QPE) 行列の固有値を、量子状態ベクトルの位相として、求めるアルゴリズムです。ハミルトニアン(つまりエネルギー変換行列)の固有値を求めることは、他の多くのアルゴリズムで用いられます。
NISQアルゴリズム
NISQアルゴリズムには、以下のものがあります。
- 量子変分アルゴリズム(Variational Quantum Eigen solver, VQE ) 量子変分原理にもとずいて、行列の最小の固有値を発見的に求めるアルゴリズムです。 量子変分原理は、行列の期待値を最小化することによって、最小の固有値がえられるという原理です。
- QAOA(Quantum Approximate Optimization Algorithm) : 量子近似最適化アルゴリズム VQEの派生系で、量子断熱計算を行うことによって、最適化問題に応用できるアルゴリズムです。
- 量子機械学習アルゴリズム SVM(サポートベクトルマシン)のカーネルや、ニューラルネットワークを量子回路に変えて、機械学習を行うアルゴリズムです。
Python と IBM Quantum, Qiskit でプログラミング
現在利用可能なNISQを用いる前提で、どのような問題が解けるのか、アルゴリズムは実際どのようなものなのかを知るために、現在利用できるフレームワークを用いたプログラムを見てみましょう。
量子コンピューティングのフレームワークとしては、以下のように多くのものがあります。この中で、資料が充実していて、実機も無料で使えることなどを総合的に判断して、今回は、IBM Qiskit とPythonをもちいて量子コンピュータのプログラミングを解説していきます。
IBM Qiskit (Quantum Information Software Kit)
- オープンソースの量子ソフトウェア開発フレームワークです。
- ハードウェアレベルの命令言語 QASM、量子ゲートを操作するローレベルAPI Terra、量子化学、最適化問題、量子機械学習などのアルゴリズムをサポートするハイレベルAPI Aqua、ノイズモデルを含むシミュレーター Aer から成り立っています。
- 豊富な資料と包括的な教科書が準備されています。ただし、教科書は、一見簡単そうに見えますが、量子物理に精通した人向けにかかれており、初心者にとっては、難易度が高いものとなっています。
- Qiskitのコミュニティ活動も盛んです。
- IBMクラウドで、5量子ビットの実機を無料で使うことができます。ただし計算に要する時間は長く、結果がでるまでに数時間かかります。5量子ビット程度の量子回路であれば、シミュレーターの方が圧倒的に早く計算が終了します。
Google Cirq
- Qiskit同様、オープンソースのNISQアルゴリズム用のフレームワークです。公式ドキュメントも豊富で、コミュニティも発達してきています。
- Google Colabでプログラムを実行できます。
Amazon AWS Braket
- 2020年に発表された比較的新らしいフレームワークです。教育資料もありますが、限られたものです。従量課金方式がとられています。
Microsoft Q# and Azure Quantum
- マイクロソフトは、プログラム言語として、Q#を採用しています。シミュレーターをクラウドで提供しています。教育資料は良いものですが、チュートリアルの数が限られています。
Rigetti Forest
- PyQuil というNISQアルゴリズムに最適化した独自のフレームワークを提供しています。RigettiやAmazon Braketのクラウドサービスでプログラムを実行できます。教育資料は限られています。
Xanadu Pennylane
- Strawberry Fields というフレームワークを提供しています。また、PennyLaneといういろんな量子コンピュータがあつかえるクロス・プラットフォームのPythonライブラリも提供されています。
blueqat
- blueqat株式会社の国産の量子コンピューティングpythonフレームワークです。クラウド経由で実機を使うことができます。チュートリアルも充実しています。
Qulacs
- 大阪大学の藤井研究室で開発され株式会社QunaSysによって新機能の開発とメンテナンスが行われています。
- Cirq, PennyLaneなどのサービスのバックエンドとして利用可能なオープンソース量子回路シミュレーターです。大きな量子回路やノイズがある量子回路にも対応しています。
IBM Quantum実行環境
IBM Quantumのアカウント作成
まず、IBM Quantum URL: https://quantum-computing.ibm.com/ にアクセスして、Create an IBMid account で、IBMidを取得してください。
IBM Quantum サインイン画面
取得したIBMidで、サインインするとIBM Quantum Welcome 画面が表示されます。API tokenは、IBM QuantumのAPIにアクセスするときに、必要になります。
IBM Quantum Welcome 画面
ここで、Launch Composer をクリックすると、下のようにGUIで量子回路の作成ができます。ここでは、Pythonを用いたプログラミングを扱いますので、詳細は割愛します。
Welcome画面で、Launch Lab をクリックすると、Jupyter Lab が起動します。標準のJupyter Lab とは、デザインが異なりますが、基本的な使い方は、同じです。Jupyter Labの使い方のは省略します。
Notebookの下のアイコンをクリックすると、Jupyter Lab が立ち上がります。その後、プログラミングを行うという流れです。

IBM Quantum ローカル実行環境
以下のようにローカルにもインストールできますが、各種モジュールのバージョン依存関係などによりエラーが発生する可能性少なからずあります。IBM Quantum lab を使うことを、推奨します。
Anacondaのインストールと環境設定
Qiskitは、Python3.6以降がサポートされており、データサイエンス用のプラットフォームAnacondaが推奨されています。Anacondaのインストールについては、ネット上にも様々な情報がありますので、ここでは省略します。
Anacondaのconda コマンドを使ってQiskit専用の仮想環境を作成することをお勧めします。Anaconda プロンプトを使って以下のように環境を作成します。環境名である ENV_NAME は、各自選んだ適当な名前に変更してください。
xxxxxxxxxxconda create -n ENV_NAME python=3新しい環境をアクティブにします。
xxxxxxxxxxconda activate ENV_NAMEpip をアップグレードします。
xxxxxxxxxxpip install --upgrade pipQiskitパッケージをインストールします。
xxxxxxxxxxpip install qiskit可視化機能やJupyter notebookを使うために、 visualization 機能を追加してインストールします。
xxxxxxxxxxpip install qiskit[visualization]Qiskit フレームワークの全体像
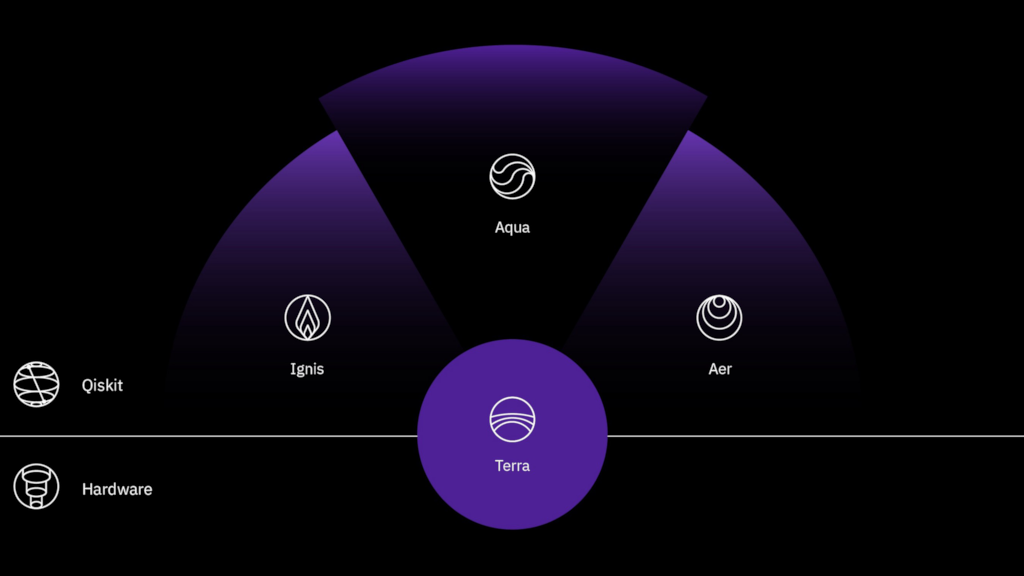
Terra
量子プログラムを実行する基盤です。いろいろなモジュールから成り立っています。以下、代表的な機能です。
- 量子回路の量子ゲート操作の演算を行い、測定結果を出力します。
- コンパイラ(トランスパイラーとも呼ばれます) 量子ゲート数と量子回路の実行時間を減らすために、量子回路の最適化を行います。
- プロバイダ 量子回路をバックエンドで実行します。
- 様々な形で可視化を行います。
Aer
Aer は、Terraでコンパイルされた回路を実行するためのC++言語で記述された 量子回路のシミュレーターです。Aerは実機で発生するエラーのノイズ・シミュレーションも含みます。3つのシミュレーターがあります。
- Qasm シミュレーター 量子回路を、ノイズがなし、またはノイズありで複数回実行し、結果を返します。
- 状態ベクトル(state vector)シミュレーター 量子回路をノイズなしで一回実行し状態ベクトルを返します。実機では、状態ベクトルは直接観測できず計測をしないといけませんが、状態ベクトルシミュレーターでは実行結果の状態ベクトルを知ることができます。あくまでシミュレーションであることに注意が必要です。
- ユニタリー・シミュレーター。 量子回路をノイズなしで、一回実行し、結果のユニタリー行列を返します。測定やリセット操作を含めることはできません。
Ignis
研究者を対象とした、エラー特定、ゲートの改良、ノイズ存在下での計算などを行うものです。
Aqua
化学や最適化、金融、AI などのアプリケーション用アルゴリズムを実装した量子計算のハイレベルAPIです。量子ゲートの操作などを意識することなく量子化学計算、量子機械学習、最適化、金融への応用などの量子コンピューティングのアプリケーションを作ることができます。
Qiskit とPython を用いた量子コンピュータのプログラミング
Qiskitのプログラムの基本的なステップ
ビルド:問題を解くための量子回路を作成します。
コンパイル:量子コンピュータの実機やシミュレーターで動作させるために回路をコンパイルします。
実行:コンパイルされた回路の演算を実行します。
分析:実行結果の統計処理を行い、実行結果を可視化します。
ビルドとコンパイルは、クラウドのIBM Quantum lab でも、ローカルにQiskit をインストールした環境でも、かまいません。ローカル環境から、実機を用いる場合は、APIを経由して、実機で計算が実行します。
プログラミングの実例
IBM Quantum にサインインして、Launch Lab をクリックし、Qiskit ノートブックを立ち上げます。セルに順次プログラムを入力し、セルを選択して、シフトキーとリターンキーを押すと、セルに入力したプログラムが実行されます。
ステップ 1 : パッケージをインポートする。
必要なパッケージをインポートし、使用するシュミレータを指定します。ここでは、Qasmシュミレータを用います。
xxxxxxxxxximport numpy as npfrom qiskit import QuantumCircuit, transpile # 量子回路のクラスとコンパイラをインポートします。from qiskit.providers.aer import QasmSimulator #Aerの回路シミュレータです。from qiskit.visualization import plot_histogram # ヒストグラム作成モジュールです。
simulator = QasmSimulator() # シュミレータとして、qasm_simulatorを設定します。ステップ 2 : 量子回路を定義する。
xxxxxxxxxxcircuit = QuantumCircuit(2, 2)2つの量子ビットと2つの古典ビットからなる回路を作成します。おのおのビットはゼロに初期化されます。
ステップ 3 : ゲートを追加する。
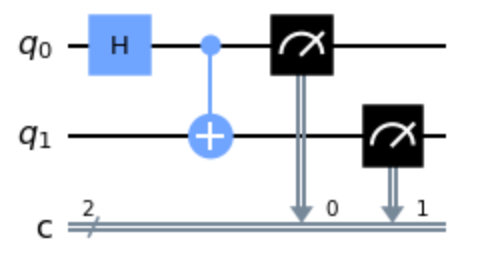
ステップ4で可視化される回路を参照するとこのプログラムの意味が、よく理解できると思います。
xxxxxxxxxxcircuit.h(0) # 量子ビット0にアダマールゲートで重ね合わせ状態をつくる。circuit.cx(0, 1) # 量子ビット0と1の間に、エンタングル状態をつくる circuit.measure([0,1], [0,1]) # 計測する。circuit.h(0) : 初期化された量子ビット0を、アダマールゲートで重ね合わせ状態をつくります。
circuit.cx(0, 1) : 量子ビット0を制御ゲート、1をターゲットゲートとしたCNOTゲートで、量子ビット0と量子ビット1を、エンタングル状態にします。
circuit.measure([0,1], [0,1]) : 測定をします。
measure(qubit, cbit) qubit: 計測する量子ビット、cbit: 計測結果を保存する古典ビット
ステップ 4: 回路を可視化する
draw()を用いて、回路を可視化します。
xxxxxxxxxxcircuit.draw()
ステップ 5: 演算のシミュレーション
シュミレータ Qiskit Aer を用いてシミュレーションを行います。シミュレーションには、qasm_simulator を使います。
xxxxxxxxxxsimulator = QasmSimulator() # シュミレータとして、qasm_simulator を使う。compiled_circuit = transpile(circuit, simulator) # 上で定義した回路をコンパイルする。job = simulator.run(compiled_circuit, shots=1000) # シミュレーションを、1000回実行する。result = job.result() # シミュレーション結果を取得する。counts = result.get_counts(circuit) # シミュレーション結果から、回数を取得する。print("\nTotal count for 00 and 11 are:",counts)シミュレーション結果
xxxxxxxxxxTotal count for 00 and 11 are: {'11': 483, '00': 517}
ノイズを含むqusm_simulotorを使って、1000回シミュレーションを繰り返して、11となるのが483回、00となるのが、517回という結果になりました。状態ベクトルは、
ステップ6: 演算結果の可視化
Qiskit には、多くの可視化のやり方が含まれていますが、ここでは、plot_histogramという関数を用いて可視化を行います。
xxxxxxxxxxplot_histogram(counts)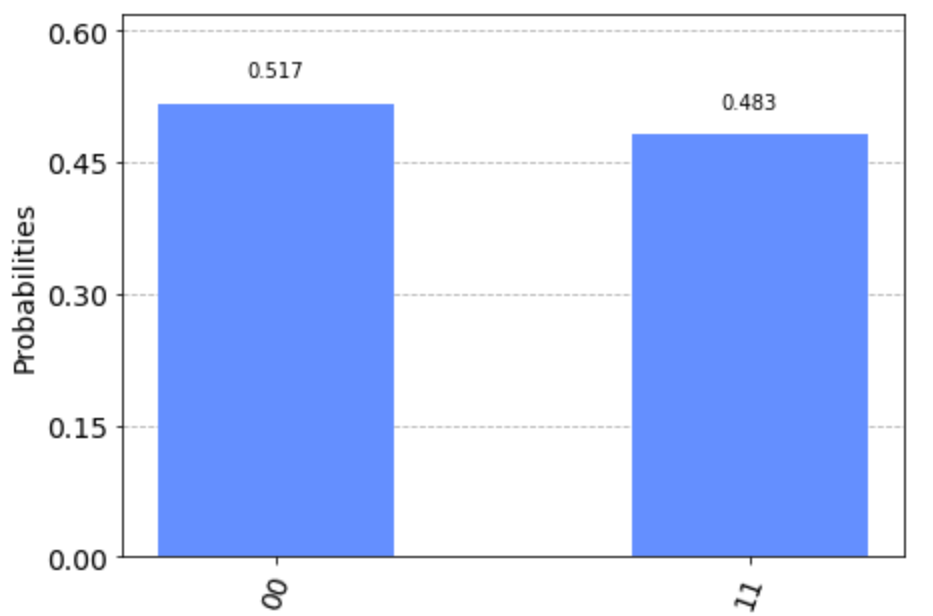
実機で実行
上では計算の実行にシュミレータを用いましたが、実機を用いて計算を実行させるには、ここまでのプログラムに、以下のプログラムを追加します。
まず、アカウント設定します。 MY_API_TOKEN には、ログイン時に表示されるAPI token をコビー&ペーストします。
xxxxxxxxxxfrom qiskit import IBMQIBMQ.save_account('MY_API_TOKEN')
Welcome画面
次に、設定したアカウントで使用可能な実機のリストを取得します。量子ビット数が1ビットのものがあり、1ビットの実機では、このプログラムは動作しませんので、稼働している実機のうち、量子ビット数が5以上のものをリストアップするようにしています。backendというのは、プログラムを実行する環境のことで、実機とシミュレーターがあります。
xxxxxxxxxxprovider = IBMQ.load_account()provider.backends(filters=lambda x: x.configuration().n_qubits >= 5 and not x.configuration().simulator and x.status().operational==True)稼働している実機のリストが表示されます。実機の稼働状況は変わりますので、リストは取得時点により変わります。
xxxxxxxxxx[<IBMQBackend('ibmq_bogota') from IBMQ(hub='ibm-q', group='open', project='main')>, <IBMQBackend('ibmq_lima') from IBMQ(hub='ibm-q', group='open', project='main')>, <IBMQBackend('ibmq_belem') from IBMQ(hub='ibm-q', group='open', project='main')>, <IBMQBackend('ibmq_quito') from IBMQ(hub='ibm-q', group='open', project='main')>, <IBMQBackend('ibmq_manila') from IBMQ(hub='ibm-q', group='open', project='main')>]次に、一番空いている実機を選択します。
xxxxxxxxxxfrom qiskit.providers.ibmq import least_busybackend_lb = least_busy(provider.backends(filters=lambda x: x.configuration().n_qubits >= 5 and not x.configuration().simulator and x.status().operational==True))print("Least busy backend: ", backend_lb)実機でプログラムを実行します。
xxxxxxxxxxfrom qiskit import executebackend = backend_lb # 最も空いている実機を使います。
result = execute(compiled_circuit, backend, shots=1000).result() #実機(backend)で1000回実行します。print(result.get_counts(circuit)) #結果の出力
plot_histogram(result.get_counts(circuit)) #結果のヒストグラムを表示します。結果
xxxxxxxxxx{'00': 504, '01': 24, '10': 24, '11': 448}
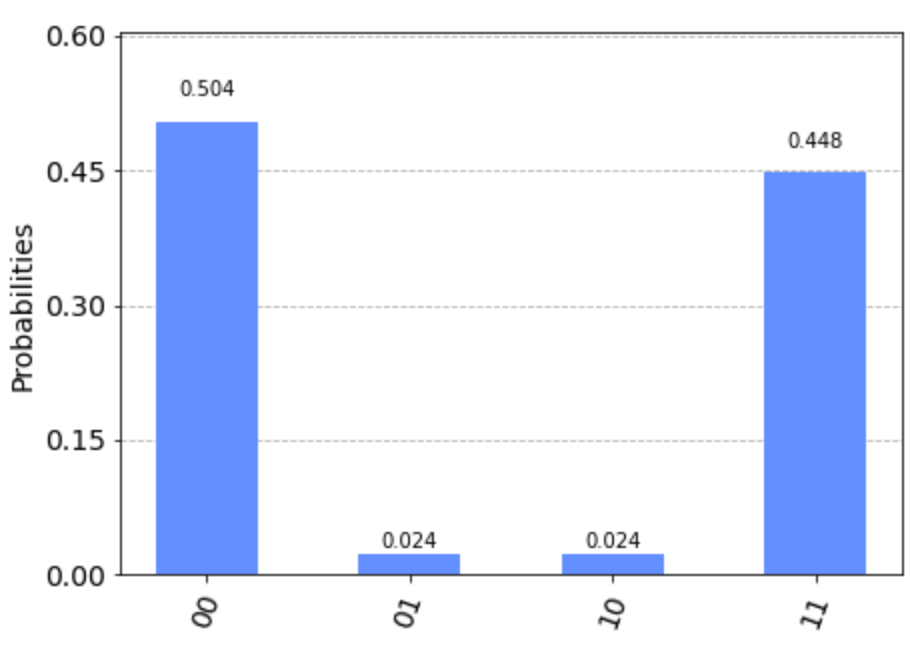
この結果を見ると、理論上は得られない
汎用量子計算
現在、稼働していて我々が使うことのできる量子コンピュータは、量子ビット数が限られ、量子ビット間の接続にも制限があり、エラー率も高いので、NISQでの実行は難しいと考えられています。したがって、ここでは、汎用量子計算の代表的なアルゴリズムの紹介にとどめます。
量子フーリエ変換(Quantum Fourier Transform, QFT)
離散フーリエ変換を量子コンピュータで実行するアルゴリズムです。離散フーリエ変換は、式(27)に従って、ベクトル
量子フーリ工変換は、式(28)に従って、量子状態
ケットベクトルを用いて、式(29)のように表すこともできます。
ユニタリ行列として表現すると、式(30)のようになります。QFTは、まとめてユニタリ行列として、扱われることがあります。
回路図は以下のようになります。
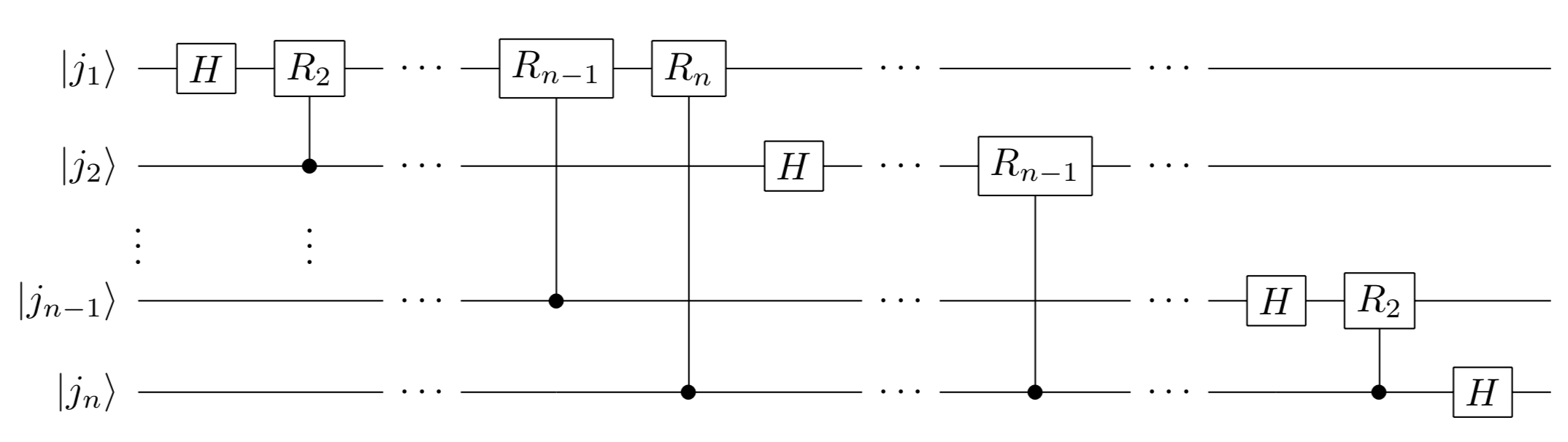
量子フーリエ変換回路図
量子位相推定(Quantum Phase Estimation, QPE)
ユニタリ行列の固有値を求めるアルゴリズムです。多くの量子アルゴリズムの構成要素として用いられます。ユ二タリ行列
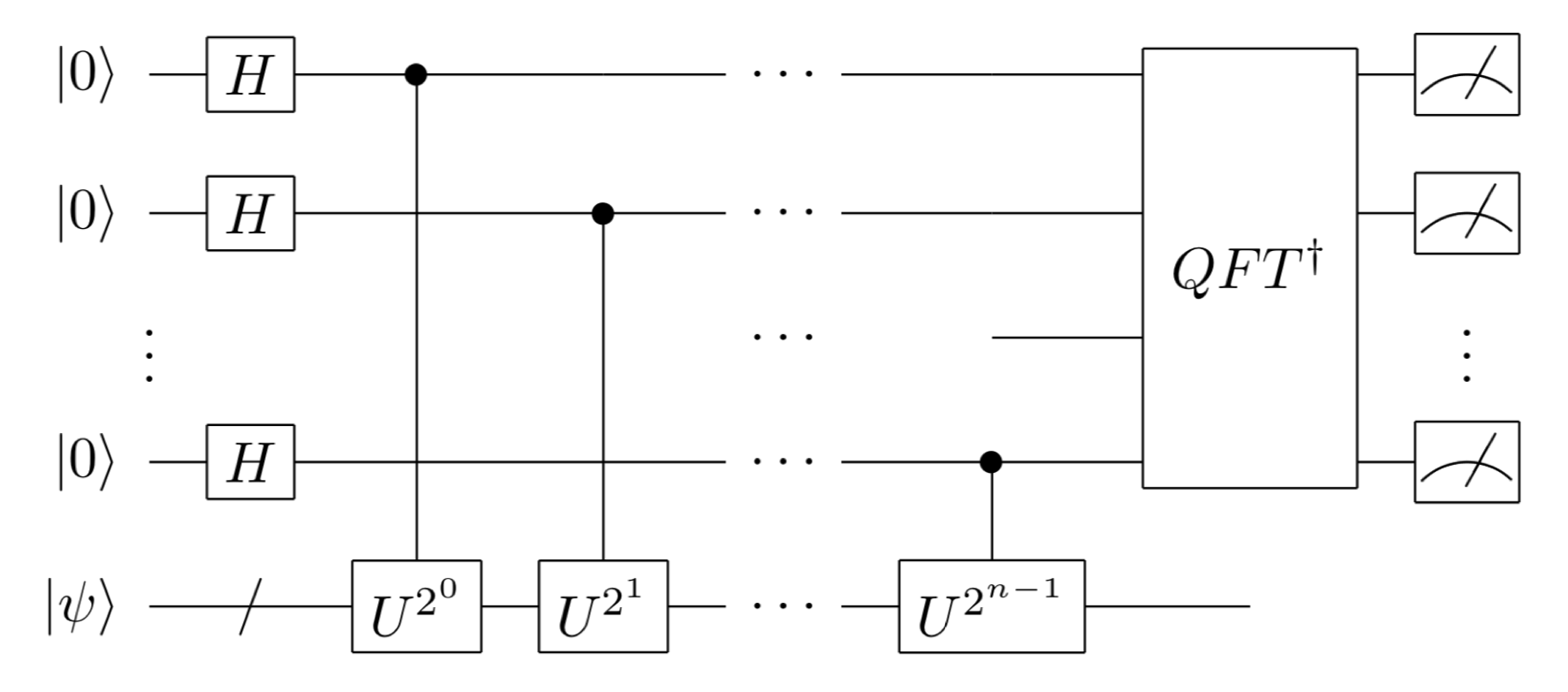
量子位相推定、QPEの応用としては、以下のようなものがあります。
- 素因数分解問題が解ける。 位数という数を推定し、素因数分解をすることができる。
- 量子系のエネルギー計算ができる。 エネルギーはハミルトニアンと呼ばれる行列の固有値によって与えらます。基底状態のエネルギーは最小の固有値、状態ベクトルは固有ベクトルで与えらます。ハミルトニアン自体はユニタリー行列ではありませんが、工夫を加えることによって、量子位相推定でエネルギーを計算することができます。
- 連立一次方程式
Shorのアルゴリズム
素因数分解を高速にとく量子アルゴリズムです。素因数分解は、自然数
この素因数問題の解き方は、
この中で、
回路は、量子位相推定と似たものですが、ここでは割愛します。
Shorのアルゴリズムを用いても、現在の量子コンピュータでは、エラーがあることと、量子ビットの数が限られていることから、すぐさま暗号が解読されるレベルの素因数分解の解を求めることはできません。
量子古典ハイブリッドアルゴリズム
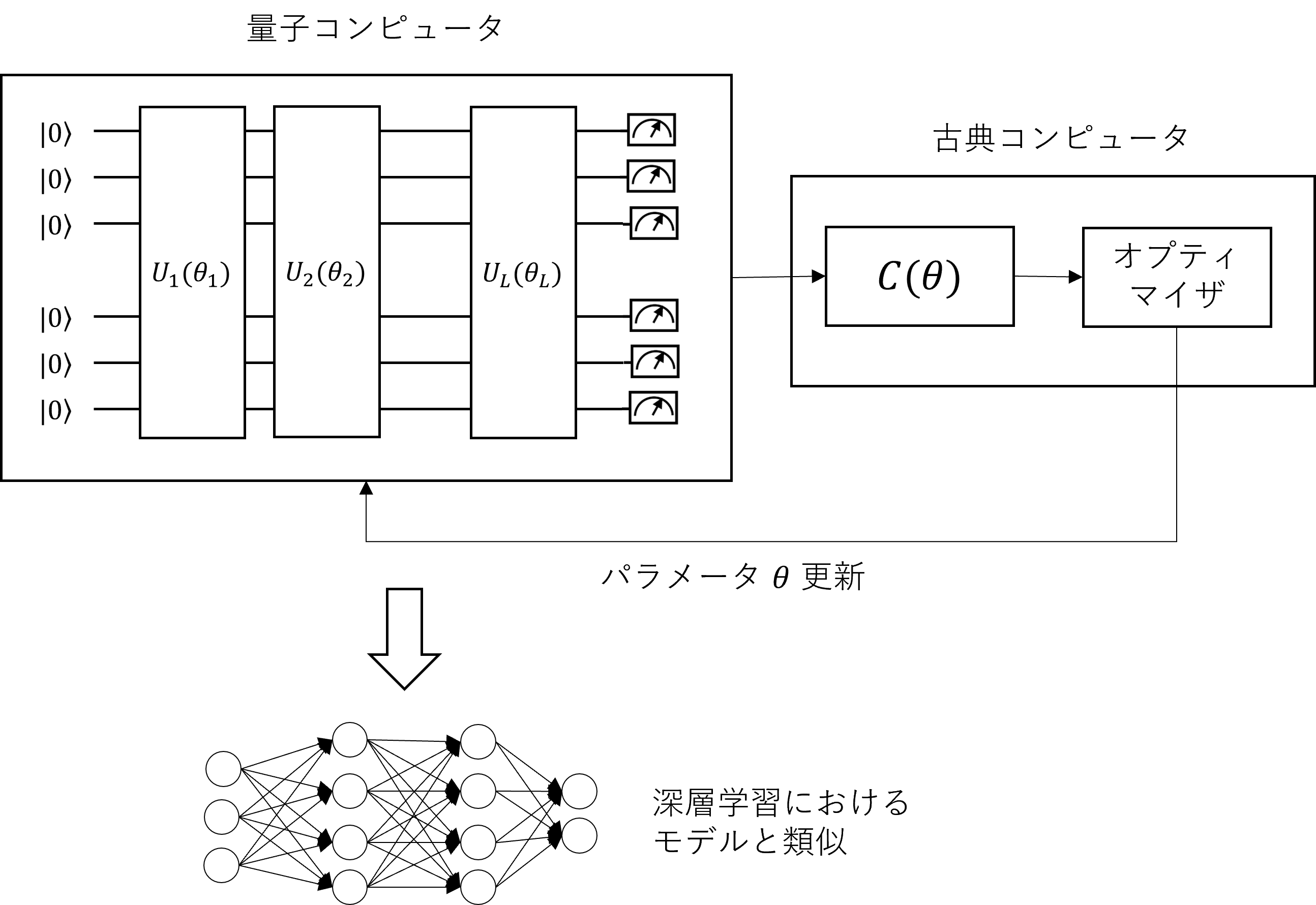
量子アルゴリズムだけのプログラムは、現時点では、エラーが多く発生し、また量子ビット数が限らることから、正しく動作しません。そこで、現在も利用可能で、量子ビット数が着実に増えているNISQ(Noisy Intermediate-Scale Quantum technology、小・中規模でノイズを含む量子コンピュータ)の活用方法の開発が盛んに行われています。その多くが、量子コンピュータでは、ビット数の少ないパラメータ付き量子回路を動作させ、古典コンピュータで、そのパラメータを探索・最適化する量子古典ハイブリッドアルゴリズムです。
量子古典ハイブリッドアルゴリズムの基本
回転角度をパラメータ
古典コンピュータの深層学習モデルより、量子回路は少ない量子ビット数でも、高い表現力を持つところから、NISQでも実行可能な実用的な計算ができることが期待されています。量子化学計算、組み合わせ最適化問題、機械学習などへの応用が進められています。
ハミルトニアンと期待値
量子状態にハミルトニアンを掛けるとエネルギーになりますので、ハミルトニアンは、量子状態をエネルギーに変換する行列だということができます。量子状態
量子変分アルゴリズム VQE
Variational Quantum Eigen solver(変分量子固有値ソルバー、VQEと略されます)は、量子状態を用いてエネルギーが最小になる基底状態を探索するアルゴリズムです。
分子の性質は、電子の状態によって決まり、その電子の状態は、シュレディンガー方程式
式(32)に示すように、VQEは、様々な量子状態
網羅的に様々な状態にたいするエネルギーを計算するのは、効率が悪いため、パラメータ付きの量子状態
- 量子コンピュータ上で量子状態
- 測定結果をもとに、古典コンピュータによって
これを
Qiskit プログラム例
ここではH-He+(水素化ヘリウムイオン)の基底エネルギーを求めてみましょう。量子コンピュータの実機では、測定を行うためにパラメータ量子状態に、ハミルトニアンを対角化するためのゲートを追加する必要がありますが、ここでは、簡単のため計算途中の量子状態を得ることができる量子状態シミュレータのプログラムを示します。 以下はdojo.qulacs.orgに掲載されたコードをQiskitで書き直したものです。
まず、必要なモジュールをインポートします。
xxxxxxxxxximport numpy as npfrom qiskit import QuantumCircuit, Aerfrom qiskit.opflow import I, X, Zfrom qiskit.circuit import Parameterfrom qiskit.quantum_info import Statevectorfrom scipy.optimize import minimizeハミルトニアンを準備します。H-He間の距離が0.9オングストロームの時のハミルトニアンです。このハミルトニアンの固有状態を計算することによって、
xxxxxxxxxxhamiltonian = ((-3.8505 * I^I) + (-0.2288 * X^I) + (-0.2288 * I^X) + (-1.0466 * Z^I) + (-1.0466 * I^Z) + (0.2613 * X^X) + (0.2288 * X^Z) + (0.2288 * Z^X) + (0.2356 * Z^Z))/2パラメータ付き量子回路を作成する関数を準備します。
xxxxxxxxxxdef PQC(phi): qc = QuantumCircuit(2) qc.rx(phi[0], 0) # 量子ビット0に角度 phi[0]のX軸回転ゲートを追加する。 qc.rz(phi[1], 0) # 量子ビット0に角度 phi[1]のZ軸回転ゲートを追加する。 qc.rx(phi[2], 1) # 量子ビット1に角度 phi[2]のX軸回転ゲートを追加する。 qc.rz(phi[3], 1) # 量子ビット1に角度 phi[3]のZ軸回転ゲートを追加する。 qc.cx(1, 0) # 量子ビット1をコントロールビットとして、量子ビット0にCNOTゲートを追加する。 qc.rz(phi[4], 1) # 量子ビット1に角度 phi[4]のZ軸回転ゲートを追加する。 qc.rx(phi[5], 1) # 量子ビット1に角度 phi[5]のx軸回転ゲートを追加する。 return qc # 作成した量子回路を返します。出来上がった量子回路を、パラメータを、
xxxxxxxxxxtheta = [Parameter('θ{:}'.format(i)) for i in range(6)] PQC(theta).draw()
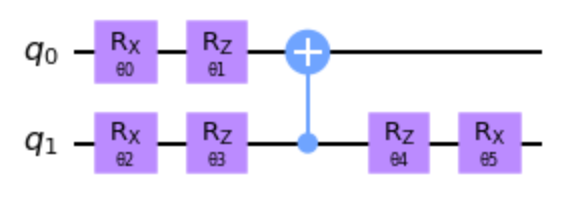
パラメータ
xxxxxxxxxxdef cost_func(theta): backend = Aer.get_backend('statevector_simulator') # 量子状態シミュレータをつかいます。 job = backend.run(PQC(theta), shots = 1024) # パラメータ付き量子回路を、パラメータを θ として計算します。 result = job.result() # 計算結果を取得します。 q_state = Statevector(result.get_statevector()) # 計算結果の状態ベクトルを取得します。 return np.real(q_state.expectation_value(hamiltonian)) # 期待値を返します。scipy の古典最適化関数 minimize で、基底エネルギをあたえる
xxxxxxxxxxinit = np.random.rand(6) # ランダムな初期値からスタートします。res = minimize(cost_func, init, method='Powell') # 損失関数が最小となる θ を求めます。cost_func(res.x) # その時の損失関数の値を求めます。計算結果です。これで、H-He間の距離が0.9オングストロームの場合の基底エネルギーが求まりました。この問題を厳密(ミルトニアンを対角化)に解いた解、-2.8626207640766816 と小数点以下第三位まで一致しています。
xxxxxxxxxx-2.8623982023201857QAOA
QAOA は、Quantum Approximate Optimization Algorithm の略で、量子近似最適化アルゴリズムと呼ばれるものです。組み合わせ最適化問題を解くためのアルゴリズムです。組み合わせ最適化問題には、巡回セールスマン問題、配車ルートの問題、集合被覆問題、ナップサック問題、スケジューリング問題などがあります。これらの問題には、意味のある時間内で正確な解を見つけることが非現実的なものが含まれるため、近似アルゴリズムが必要となります。このアルゴリズムを理解するには、量子断熱計算と呼ばれる知識が必要ですが、ここではQAOAのアルゴリズムの紹介と使い方の説明をすることにとどめます。
- 組み合わせ最適化問題とは、いろんな制約条件のもとで、数多くの選択肢の中から、目的となる指標(コスト関数)を最も小さくする変数の組合せを求めることです。
- 問題をこコスト関数と制約条件からなるモデルで表すことを、定式化するといいます。
まず、0か1 の値をとる
初期状態をつくるハミルトニアンを
ここで
初期状態
そして、
Qiskit プログラム例 Maxcut
手順は、以下の通りです。
- 問題の定式化
- コスト関数に変換
- 量子回路の作成
- 量子回路と古典オプティマイザをもちいて最適なパラメータを求める
- 得られたパラメータでQAOA回路をつくり結果を分析する。
まず、必要なパッケージをインポートします。
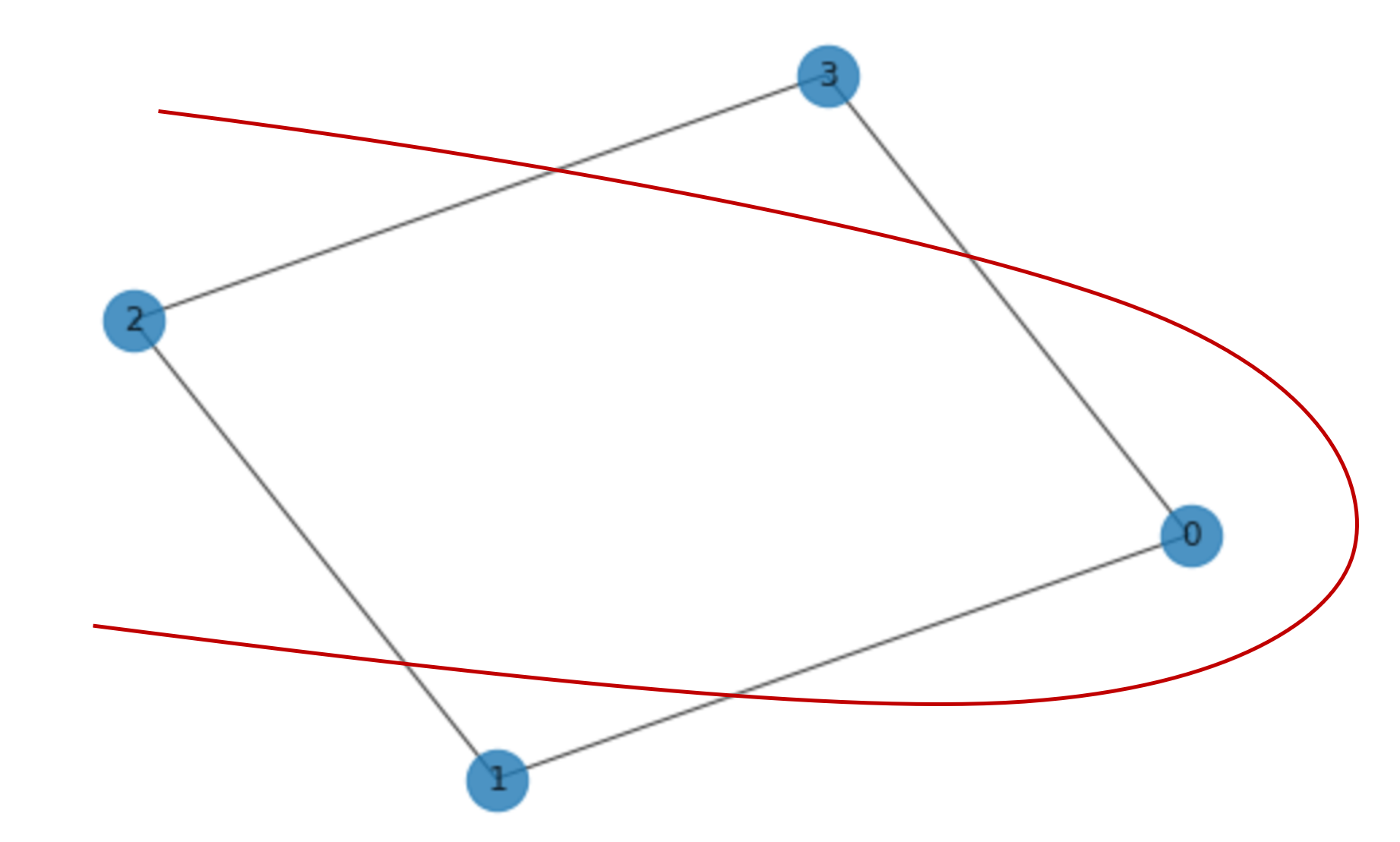
xxxxxxxxxximport networkx as nxfrom qiskit import QuantumCircuit, ClassicalRegister, QuantumRegisterfrom qiskit import Aer, executefrom qiskit.circuit import Parameter4個の頂点
Python のnetworkxというモジュールでグラフを作成し描画するとこのようになります。
xxxxxxxxxxG = nx.Graph() # 空のグラフを用意する。G.add_nodes_from([0, 1, 2, 3]) # 頂点を追加する。G.add_edges_from([(0, 1), (1, 2), (2, 3), (3, 0)]) # 辺を追加する。nx.draw(G, with_labels=True, alpha=0.8, node_size=500) # グラフを描画する。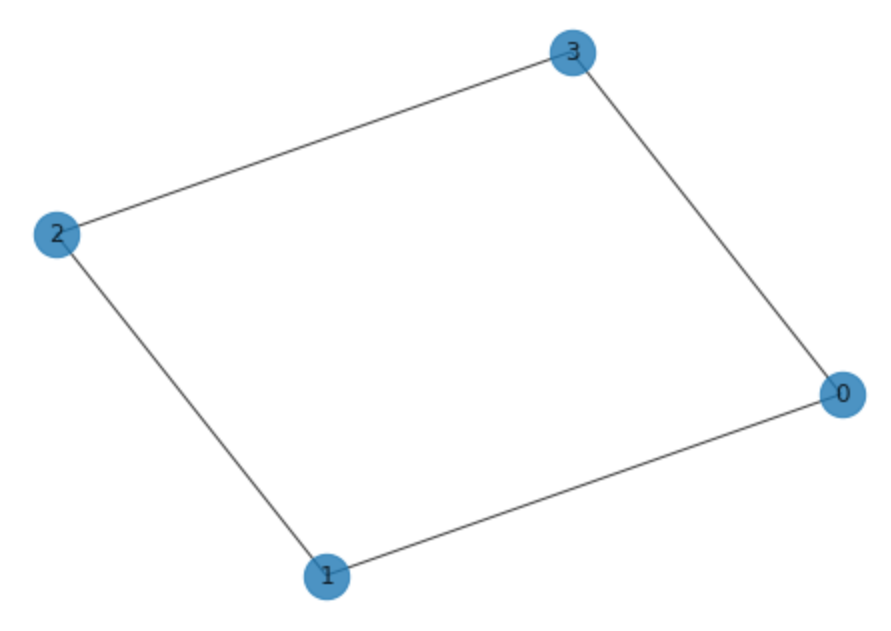
このグラフ
このような形式は、QUBO (Quadratic Unconstrained Binary Optimization) と呼ばれます。
これをハミルトニアンに、変換するには、
この問題のグラフでは、式(38)のようになります。
初期状態としては、式(40)の通り、
xxxxxxxxxxdef maxcut_obj(x, G): # 2つのグループに分割した結果xに対して、辺の数を返す関数です。 # 辺の数は負の数として返され、それを最小化します。 # 頂点が同じグループに属さないとき、その頂点間の辺がカットされます。 # 下のcompute_expectationで使われます。 obj = 0 for i, j in G.edges(): if x[i] != x[j]: obj -= 1 return obj
def compute_expectation(counts, G): # 計測結果countsから、辺の数の期待値を計算する関数です。 # bitstring は、どのようにグループ分けするかの結果、counts は、そのグループ分けがされた回数です。 # 繰り返し回路を実行した結果の辺の数の期待値(平均値)を返します。 avg = 0 sum_count = 0 for bitstring, count in counts.items(): obj = maxcut_obj(bitstring, G) avg += obj * count sum_count += count return avg/sum_count
def create_qaoa_circ(G, theta): # グラフGに対応し、パラメータθ(β,γ)をもつQAOA回路をつくる関数です。 nqubits = len(G.nodes()) # ノードの数 p = len(theta)//2 # ユニタリ行列の繰り返し回数 qc = QuantumCircuit(nqubits) # nqubitsの量子回路を準備する。 beta = theta[:p] # パラメータβ gamma = theta[p:] # パラメータγ # 初期状態を設定するためアダマールゲートを追加して重ね合わせ状態をつくります。 for i in range(0, nqubits): qc.h(i) # アダマールゲートを追加する。 for irep in range(0, p): # 問題のハミルトニアン UC(γ) for pair in list(G.edges()): qc.rzz(2 * gamma[irep], pair[0], pair[1])
# ミキサ・ハミルトニアン UB(β) for i in range(0, nqubits): qc.rx(2 * beta[irep], i) # 計測します。 qc.measure_all() return qc
def get_expectation(G, p, shots=512): # グラフGをユニタリ行列の繰り返し回数pで計算をおこないます。 backend = Aer.get_backend('qasm_simulator') backend.shots = shots def execute_circ(theta): # 上のcreate_qaoa_circ関数をもちいて量子回路をつくります。 qc = create_qaoa_circ(G, theta) # 作成した量子回路を動作させ指定したショット数だけ計算を実行し、各量子ビットのカウント値を求めます。 counts = backend.run(qc, seed_simulator=10, nshots=512).result().get_counts() # カウント値から、辺の数期待値を計算します。 # 辺の数はマイナスで数えられているので、この期待値を最小化することで問題を解きます。 return compute_expectation(counts, G) return execute_circ作成される回路は次の通りです。
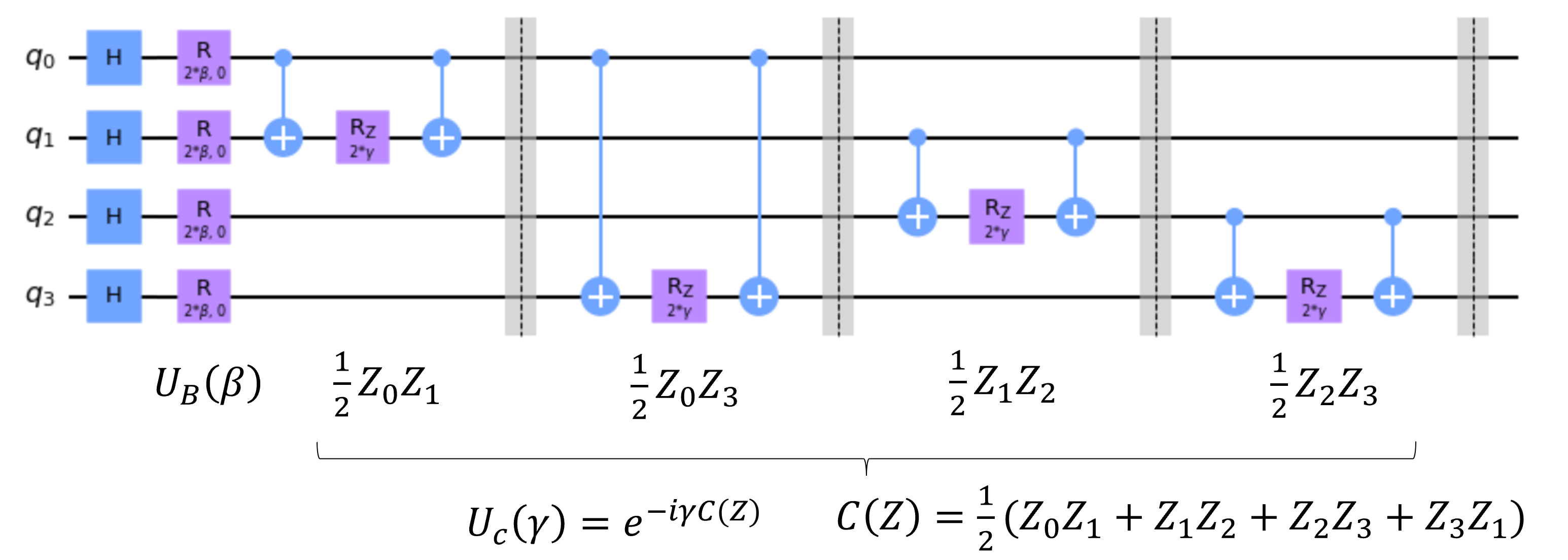
Maxcut 回路図
次に、scipyの古典最適化モジュールで、最適値を求めます。
xxxxxxxxxxfrom scipy.optimize import minimize
expectation = get_expectation(G, p=1) # ユニタリ行列の繰り返し回数 1 での期待値計算を対象とします。res = minimize(expectation, [1.0, 1.0], method='COBYLA') # β、γの初期値を、1.0, 1.0 として、辺の数の期待値を最小化する最適値を求めます。# ここでは、COBYLA という最適化手法を用います。
res # 結果を表示します。fun: -2.994140625 maxcv: 0.0 message: 'Optimization terminated successfully.' nfev: 30 status: 1 success: True x: array([1.9793337 , 1.16663483])
最適化が終了し、x すなわち
次に、最適化されたパラメータ
xxxxxxxxxxfrom qiskit.visualization import plot_histogram
backend = Aer.get_backend('aer_simulator') #バックエンドとしてaer_simulator を用います。backend.shots = 512
qc_res = create_qaoa_circ(G, res.x) # 最適化されたパラメータ β、γ でQAOA回路を作ります。counts = backend.run(qc_res, seed_simulator=10).result().get_counts() # 量子回路計算を実行します。
plot_histogram(counts)
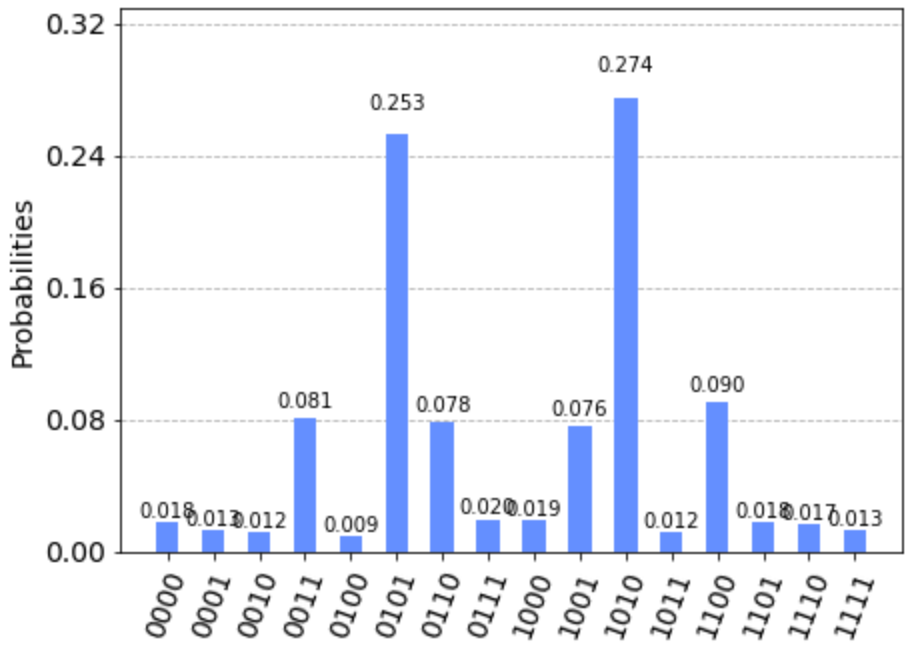
ビット列「0101」と「1010」(すなわち頂点0と頂点2、頂点3と頂点1でカットする)の確率が最も高く、図25に示すように、最大の辺の数が、4つである分割となっています。
Maxcut の計算結果
このプログラムを見て、複雑だと思われた読者も多いと思いますが、心配はいりません。IBM Qiskit には、QAOAのゲート回路などをプログラミングすることなく問題を解くことができるハイレベルAPIが準備されています。
[上記のプログラムは、IBM qiskit テキストブックの Solving combinatorial optimization problems using QAOA https://qiskit.org/textbook/ch-applications/qaoa.html の一部で、コメントを日本語に修正しています。]
Qiskitを用いてVQE,QAOA で実問題を解く
ここでは、IBM quantum challenge fall 2021(https://github.com/qiskit-community/ibm-quantum-challenge-fall-2021) から、興味深い実問題の解法を紹介します。Python と Qiskit を用いたプログラムです。Qiskit のハイレベルAPIを用いることによって、実問題を簡単に解くことができます。
ポートフォリオ最適化
ポートフォリオとは、株式などの金融資産の組み合わせのことです。ポートフォリオ最適化のゴールは、リスクを最小化し、リターンを最大化することですが、リスクとリターンは通常トレードオフの関係にあります。積極的に大きなリターンを得ようとするなら、リスクが大きい金融資産を多く所有し、手堅く運用したいなら、リスクが小さい金融資産に多くを配分することになります。最適な配分を決めることは、そう簡単ではありません。
最適な配分を決める方法として、現代ポートフォリオ理論というものがあります。リスクを避けながら、いかにリターンを大きくするかという方針にもとづいて最適な配分を行うというものです。
そのためには、以下のことを行います。
- 過去のデータに基づいて、ポートフォリオの銘柄の平均、分散と相関を計算する。
- リスクを抑えつつリターンを大きくする銘柄の重みと期待リターンを計算する。
四銘柄のポートフォリオ最適化問題
こでは、株式4銘柄の、リスクとリターンの間のトレードオフを最小化する配分を見つけることを問題とします。
問題の定式化
として、(41)のように定式化できます。第一項が、ポートフォリオのリスク(保有する銘柄間の共分散を足し合わせるたものに保有する銘柄数を足したもの)にリスクファクタを掛けたもの、第二項がポートフォリオのリターンを表しています。つまり、リスクを抑えつつ、リターンを大きくしようとすることを数式化したものです。。
ゴール
どの銘柄を選ぶか、選ばないかの
仮定
問題を簡単にするため、以下の仮定を置きます。
- すべての銘柄の価格は同じ。
- 予算
ライブラリのインポート
xxxxxxxxxxfrom qiskit import Aerfrom qiskit.algorithms import VQE, QAOA, NumPyMinimumEigensolverfrom qiskit.algorithms.optimizers import *from qiskit.circuit.library import TwoLocalfrom qiskit.utils import QuantumInstancefrom qiskit.utils import algorithm_globalsfrom qiskit_finance import QiskitFinanceErrorfrom qiskit_finance.applications.optimization import PortfolioOptimizationfrom qiskit_finance.data_providers import *from qiskit_optimization.algorithms import MinimumEigenOptimizer from qiskit_optimization.applications import OptimizationApplicationfrom qiskit_optimization.converters import QuadraticProgramToQuboimport numpy as npimport matplotlib.pyplot as plt%matplotlib inlineimport datetimeimport warningsfrom sympy.utilities.exceptions import SymPyDeprecationWarningwarnings.simplefilter("ignore", SymPyDeprecationWarning)時系列データ(金融データ)の生成
RandomDataProviderクラスを使って、4銘柄のランダムな値動きデータを作成します。バジェットを2として、4銘柄から2銘柄を選択することとし、リスクファクタを0.5にします。
xxxxxxxxxx# 銘柄とリスクファクターのパラメータを設定します。num_assets = 4 # 銘柄数 4q = 0.5 # リスクファクター 0.5budget = 2 # バジェットは、2seed = 132
# 4銘柄のランダムな値動き時系列データを作成します。stocks = [("STOCK%s" % i) for i in range(num_assets)]data = RandomDataProvider(tickers=stocks, start=datetime.datetime(1955,11,5), end=datetime.datetime(1985,10,26), seed=seed)data.run()xxxxxxxxxx#4データをプロットします。for (cnt, s) in enumerate(data._tickers): plt.plot(data._data[cnt], label=s)plt.legend()plt.xticks(rotation=90)plt.xlabel('days')plt.ylabel('stock value')plt.show()期待リターンと共分散行列の計算
get_period_return_mean_vector() メソッドで、期待リータンが計算できます。
xxxxxxxxxxmu = data.get_period_return_mean_vector() # おのおのの銘柄の期待されるリターンを返します。print(mu)[1.59702144e-04 4.76518943e-04 2.39123234e-04 9.85029012e-05]
4銘柄に対しての期待するリターンが、求まりました。次に、共分散行列の計算を行い、表示します。
xxxxxxxxxx# 共分散行列 Σ のプロットsigma = data.get_period_return_covariance_matrix() # 4つの銘柄の共分散行列を返します。fig, ax = plt.subplots(1,1)im = plt.imshow(sigma, extent=[-1,1,-1,1])x_label_list = ['stock3', 'stock2', 'stock1', 'stock0']y_label_list = ['stock3', 'stock2', 'stock1', 'stock0']ax.set_xticks([-0.75,-0.25,0.25,0.75])ax.set_yticks([0.75,0.25,-0.25,-0.75])ax.set_xticklabels(x_label_list)ax.set_yticklabels(y_label_list)plt.colorbar()plt.clim(-0.000002, 0.00001)plt.show()共分散行列
- 2つの銘柄が同時に増加・減少すれば、共分散の値は正の値になります。
- 一方が上昇し、他方が下降した場合、共分散の値は負になります。
違う動きをする銘柄に投資することはリスクを減らす効果があります。
Qiskit Finance のポートフォリオ最適化クラス
PortfolioOptimization クラスを使うと、
xxxxxxxxxxportfolio = PortfolioOptimization(expected_returns=mu, covariances=sigma, risk_factor=q, budget=budget, bounds=None)qp = portfolio.to_quadratic_program() # μ,Σ、qからQUBOを作成し返します。print(qp)定式化した結果が出力されます。
Minimize (最小化するコスト関数、x_0, x_1,x_2,x_3 が変数) obj: - 0.000159702144 x_0 - 0.000476518943 x_1 - 0.000239123234 x_2 - 0.000098502901 x_3 + [ 0.000048831990 x_0^2 - 0.000002157372 x_0x_1 - 0.000004259230 x_0x_2 + 0.000001413200 x_0x_3 + 0.000997360142 x_1^2 + 0.000007031887 x_1x_2 + 0.000000737432 x_1x_3 + 0.000287365468 x_2^2 + 0.000006416382 x_2x_3 + 0.000192316728 x_3^2 ]/2 Subject To (制約条件) c0: x_0 + x_1 + x_2 + x_3 = 2
Bounds (値の範囲) 0 <= x_0 <= 1 0 <= x_1 <= 1 0 <= x_2 <= 1 0 <= x_3 <= 1
Binaries (バイナリ変数) x_0 x_1 x_2 x_3
Minimum Eigen Optimizer(最小固有値オプティマイザー)
このポートフォリオ最適化問題は、ハミルトニアンの基底状態を求める問題として解くことができます。ハミルトニアンを考えると、シミュレーションしたいシステムのエネルギー関数と考えることができます。そのためには、図に示すように、QUBOで定式化したものを、イジングモデルと呼ばれる数学モデルで表現し、さらにハミルトニアンに変換するという複雑な計算を行わないといけません。Qiskit は、これらの変換を自動的にやってくれます。MinimumEigenOptimizer(最小固有値オプティマイザー)が、QUBOをハミルトニアンに変換し、VQEやQAOAなどを呼び出して基底状態を計算し、最適化の結果を返します。
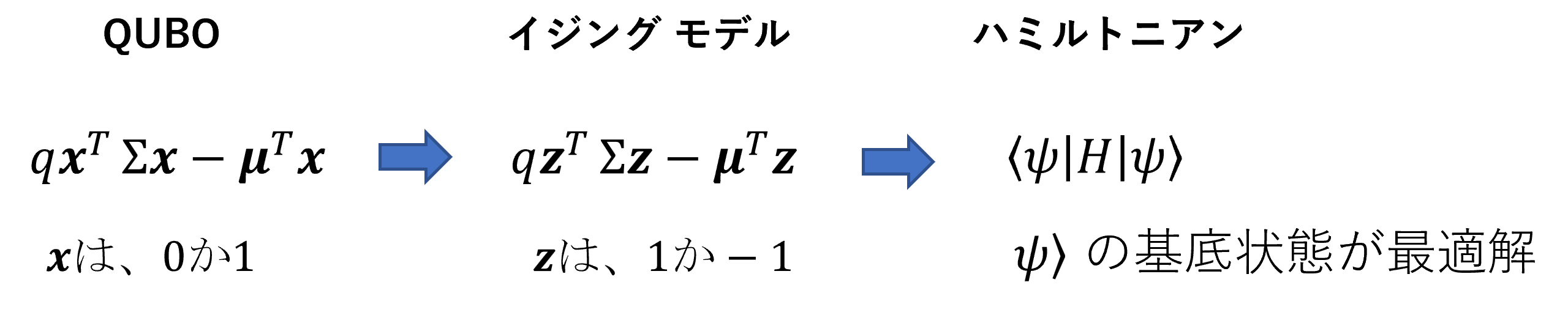
最適化問題の解法の流れ
古典コンピュータの最適化アルゴリズムで問題を解く
この規模の問題は、古典コンピュータの最適化アルゴリズムで解くことができます。
xxxxxxxxxxexact_mes = NumPyMinimumEigensolver() # Numpy最小固有値ソルバーを使います。exact_eigensolver = MinimumEigenOptimizer(exact_mes) # 最小固有値オプティマイザーに、Numpy最小固有値ソルバーを使う設定をします。result = exact_eigensolver.solve(qp) # Step 4. で作成したQUBOを解きます。print(result)以下のような結果がでました。
optimal function value: -0.00023285626449450202 (コスト関数の最適値) optimal value: [1. 0. 1. 0.] (最適値つまりどの銘柄を保有するかは、$x_0 =1, x_1 = 0, x_2 = 1, x_3 = 0) status: SUCCESS (計算は成功)
VQEを使ったソリューション
xxxxxxxxxxoptimizer = SLSQP(maxiter=1000) # 古典オプティマイザとして、SLSQPを用います。algorithm_globals.random_seed = 1234backend = Aer.get_backend('statevector_simulator') # 状態ベクトルシミュレータを用います
# 図27に示す量子回路と古典オプティマイザからなるVQEを構成します。ry = TwoLocal(num_assets, 'ry', 'cz', reps=1, entanglement='full') quantum_instance = QuantumInstance(backend=backend, seed_simulator=seed, seed_transpiler=seed)vqe = VQE(ry, optimizer=optimizer, quantum_instance=quantum_instance)
vqe_meo = MinimumEigenOptimizer(vqe) #最小固有値オプティマイザーに、上で作成したvqeを使う設定をします。result = vqe_meo.solve(qp) # Step 4. で作成したQUBOを解きます。print(result)optimal function value: -0.00023285626449450202 (コスト関数の最適値) optimal value: [1. 0. 1. 0.] (最適値つまりどの銘柄を保有するかは、x_0 =1, x_1 = 0, x_2 = 1, x_3 = 0) status: SUCCESS (計算は成功)
古典コンピュータの最適化アルゴリズムと同じ答えが得られました。
用いている量子回路は、次の通りです。
QAOAを使ったソリューション
xxxxxxxxxxoptimizer = SLSQP(maxiter=1000) # 古典オプティマイザとして、SLSQPを用います。algorithm_globals.random_seed = 1234backend = Aer.get_backend('statevector_simulator') # バックエンドとして状態ベクトルシュミレータを使います。
quantum_instance = QuantumInstance(backend=backend, seed_simulator=seed, seed_transpiler=seed)qaoa = QAOA(optimizer=optimizer, reps=1, quantum_instance=quantum_instance) #qaoaを構成します。
qaoa_meo = MinimumEigenOptimizer(qaoa) #最小固有値オプティマイザーに、上で作成したqaoaを使う設定をします。result2 = qaoa_meo.solve(qp) # Step 4. で作成したQUBOを解きます。print(result2)optimal function value: -0.00023285626449450202 (コスト関数の最適値) optimal value: [1. 0. 1. 0.] (最適値つまりどの銘柄を保有するかは、$x_0 =1, x_1 = 0, x_2 = 1, x_3 = 0) status: SUCCESS (計算は成功)
古典コンピュータの最適化アルゴリズムと同じ答えが得られました。
このように、Qiskit では、ポートフォリオ最適化を、量子回路を強く意識することなく解くことができます。VQEでは、パラメータ付き量子回路の設定をしなければなりませんが、QAOAでは、アルゴリズム自体にパラメータ付き量子回路が含まれているため、その必要性はありません。
このプログラムは、ibm-quantum-challenge-fall-2021challenge-1 のコメントを日本語に修正したものです。
ナップザック問題
ナップサック問題は、図28に示すように、それぞれに重量と価値がある品物リストと、運べる重量の最大値が決められたナップサックがあったとして、なるべく多くの価値になるように品物を選ぶ問題です。
 Image
Image
ナップザック問題 図:Knapsack.svg.
一般的なナップサック問題をQAOAで解く
問題:容量18のナップサックと5つの荷物があります。荷物の各重量𝑊Wが
xxxxxxxxxxfrom qiskit_optimization.algorithms import MinimumEigenOptimizerfrom qiskit import Aerfrom qiskit.utils import algorithm_globals, QuantumInstancefrom qiskit.algorithms import QAOA, NumPyMinimumEigensolverimport numpy as np動的計画法(古典コンピュータによる計算)
古典コンピュータで、正確な解を見つけるための典型的な方法である動的計画法によるプログラムは、次のとおりです。この手法の時間計算量は、荷物の数×ナップサックの最大重量に比例します。この場合は、組み合わせの数が限られているため、短時間で問題を解くことができますが、荷物の数が膨大になると、この方法を使うことは、現実的ではありません。 動的計画法というのは、「対象となる問題を複数の部分問題に分割し、部分問題の計算結果を記録しながら解いていく手法」の総称ですが、ここでは古典コンピュータでも、このように解けるというのにとどめ、アルゴリズムの詳細説明は長くなりますので、省略します。
xxxxxxxxxxval = [5,6,7,8,9] # 荷物の価値wt = [4,5,6,7,8] # 重量W = 18 # ナップザックで運べる最大重量xxxxxxxxxxdef dp(W, wt, val, n): k = [[0 for x in range(W + 1)] for x in range(n + 1)] for i in range(n + 1): for w in range(W + 1): if i == 0 or w == 0: k[i][w] = 0 elif wt[i-1] <= w: k[i][w] = max(val[i-1] + k[i-1][w-wt[i-1]], k[i-1][w]) else: k[i][w] = k[i-1][w] picks=[0 for x in range(n)] volume=W for i in range(n,-1,-1): if (k[i][volume]>k[i-1][volume]): picks[i-1]=1 volume -= wt[i-1] return k[n][W],picks
n = len(val)print("optimal value:", dp(W, wt, val, n)[0])print('\n index of the chosen items:')for i in range(n): if dp(W, wt, val, n)[1][i]: print(i,end=' ')optimal value: 21
index of the chosen items: 1 2 3
計算結果として、荷物1(価値6,重さ5)と2(価値7,重さ6)と3(価値8,重さ7)を運べば、運べる価値は、21という結果がでました。
QAOAによる解法
Qiskitは、ナップサック問題を含むさまざまな最適化問題のアプリケーションクラスを提供しているため、様々な最適化問題を量子コンピューターで簡単に試すことができます。ここでは、Knapsack問題のアプリケーションクラスを使用します。
xxxxxxxxxxfrom qiskit_optimization.applications import Knapsack # Kanpsackクラスをインポートします。ナップサック問題をQAOAで解く最適化問題として解くには、この問題を定式化しQUBOを作成する必要があります。
xxxxxxxxxxdef knapsack_quadratic_program(): # Knapsack()のパラメーターとしてvalues, weights, max_weightを入れる。 prob = Knapsack(values = val, weights = wt, max_weight=W) # to_quadratic_programはknapsack問題のQUBOを生成します kqp = prob.to_quadratic_program() return prob, kqp
prob,quadratic_program=knapsack_quadratic_program()quadratic_programMaximize (最大化するコスト関数、x_0, x_1,x_2,x_3,x_4 が変数なので運べる総価値) obj: 5 x_0 + 6 x_1 + 7 x_2 + 8 x_3 + 9 x_4 Subject To (制約条件、総重量が18以下) c0: 4 x_0 + 5 x_1 + 6 x_2 + 7 x_3 + 8 x_4 <= 18
Bounds (値の範囲) 0 <= x_0 <= 1 0 <= x_1 <= 1 0 <= x_2 <= 1 0 <= x_3 <= 1 0 <= x_4 <= 1
Binaries (バイナリ変数) x_0 x_1 x_2 x_3 x_4
このように、Kanpsackクラスを用いて、ナップザック問題のQUBOが作成できました。
古典コンピュータによる最適化のNumPyMinimumEigensolverを使用しても、最適化ができます。また、QAOAを適用することもできます。
xxxxxxxxxx# Numpy Eigensolvermeo = MinimumEigenOptimizer(min_eigen_solver=NumPyMinimumEigensolver()) # Numpy最小固有値ソルバーを使います。result = meo.solve(quadratic_program) #作成したQUBOを解きます。print('result:\n', result)print('\n index of the chosen items:', prob.interpret(result)) result: optimal function value: 21.0 optimal value: [0. 1. 1. 1. 0.] status: SUCCESS
index of the chosen items: [1, 2, 3]
計算結果として、荷物1(価値6,重さ5)と2(価値7,重さ6)と3(価値8,重さ7)を運べば、運べる価値は、21という結果がでました。
xxxxxxxxxx# QAOAseed = 123algorithm_globals.random_seed = seed# qasmシュミレータを準備します。qins = QuantumInstance(backend=Aer.get_backend('qasm_simulator'), shots=1000, seed_simulator=seed, seed_transpiler=seed)
#最小固有値オプティマイザーに、ソルバーとしてqaoa、バックエンドとして、上のqinsを使う設定をします。meo = MinimumEigenOptimizer(min_eigen_solver=QAOA(reps=1, quantum_instance=qins)) result = meo.solve(quadratic_program) # 問題を解きます。print('result:\n', result)print('\n index of the chosen items:', prob.interpret(result)) result: optimal function value: 21.0 optimal value: [0. 1. 1. 1. 0.] status: SUCCESS
index of the chosen items: [1, 2, 3]
計算結果として、荷物1(価値6,重さ5)と2(価値7,重さ6)と3(価値8,重さ7)を運べば、運べる価値は、21という結果がでました。
QAOAは近似解のため、QAOAによる解が常に最適であるとは限らないことには注意が必要です。
蓄電池システムの収益最大化
蓄電池システムは、再生可能エネルギー(風力や太陽光など)を、蓄電池に充電し、決められた時間枠に電力網に電力を供給するものです。蓄電池システムの収益を最適化するためには、価格予測に基づいた市場での収益(価値)と、予想される電池の経年劣化(コスト)の両方を考慮して、各時間枠においてどの市場で電力を販売するのかを選択する必要があります。
問題設定
2つの市場
- 日々の収益
- 電池の日々の劣化(サイクル数)
問題は、
電池による収益の最適化をQAOAで解く
パラメータを設定する
xxxxxxxxxxL1 = [5,3,3,6,9,7,1] # 収益 λ1L2 = [8,4,5,12,10,11,2] # 収益 λ2C1 = [1,1,2,1,1,1,2] # 劣化 c1C2 = [3,2,3,2,4,3,3] # 劣化 c2C_max = 16 # C max問題をナップザック問題として定式化する
xxxxxxxxxxdef knapsack_argument(L1, L2, C1, C2, C_max): # 問題をナップザック問題として定式化する。収益・劣化とも、M1が小さいので、M1を基準として考える values = list(map(lambda x, y: x - y, L2, L1)) # 収益 λ2 - 収益 λ1 のリストを生成 weights = list(map(lambda x, y: x - y, C2, C1)) # 劣化 c2 - 劣化 c1 のリストを作成 max_weight = C_max - sum(C1) # C_max から C1の合計を引く return values, weights, max_weight values, weights, max_weight = knapsack_argument(L1, L2, C1, C2, C_max)print(values, weights, max_weight)#定式化した問題を、quboに変換する。prob = Knapsack(values = values, weights = weights, max_weight = max_weight)qp = prob.to_quadratic_program()qp[3, 1, 2, 6, 1, 4, 1] [2, 1, 1, 1, 3, 2, 1] 7 (収益、劣化、最大劣化)
Maximize (最大化するコスト関数、収益) obj: 3 x_0 + x_1 + 2 x_2 + 6 x_3 + x_4 + 4 x_5 + x_6 Subject To (制約条件、劣化) c0: 2 x_0 + x_1 + x_2 + x_3 + 3 x_4 + 2 x_5 + x_6 <= 7
Bounds (値の範囲) 0 <= x_0 <= 1 0 <= x_1 <= 1 0 <= x_2 <= 1 0 <= x_3 <= 1 0 <= x_4 <= 1 0 <= x_5 <= 1 0 <= x_6 <= 1
Binaries (バイナリ変数) x_0 x_1 x_2 x_3 x_4 x_5 x_6
QAOAを用いて問題を解く
xxxxxxxxxx# QAOAseed = 123algorithm_globals.random_seed = seed# qasmシュミレータを準備します。qins = QuantumInstance(backend=Aer.get_backend('qasm_simulator'), shots=1000, seed_simulator=seed, seed_transpiler=seed)
#最小固有値オプティマイザーに、ソルバーとしてqaoa、バックエンドとして、上のqinsを使う設定をします。meo = MinimumEigenOptimizer(min_eigen_solver=QAOA(reps=1, quantum_instance=qins))result = meo.solve(qp) # 問題を解きます。print('result:', result.x)
item = np.array(result.x)revenue=0for i in range(len(item)): # 総収益を計算します。 if item[i]==0: revenue+=L1[i] else: revenue+=L2[i]
print('total revenue:', revenue)result: [1. 1. 1. 1. 0. 1. 0.] (販売する市場は、M2, M2, M2, M2, M1, M2, M1 という結果です。) total revenue: 50 (総収益は、50です。)
解答が求まりました。
[このプログラムは、ibm-quantum-challenge-fall-2021(https://github.com/qiskit-community/ibm-quantum-challenge-fall-2021) challenge-4 の一部のプログラムのコメントを日本語に修正したものです。]
量子機械学習
量子古典ハイブリッド機械学習
量子古典ハイブリッドアルゴリズムの基本で見たように、パラメータ付き量子回路を用いたVQE、QAOAは機械学習と似たたアルゴリズムです。つまり、量子コンピューティングは、機械学習にも応用が可能です。もちろん、古典コンピューティングと量子コンピューティングは、違いますので、その差を埋める必要があります。
1. 入力データの量子状態へのエンコーディング
まず、入力データを量子状態にエンコーディングしないといけません。入力データに対応した回転ゲート操作(図29)をします。
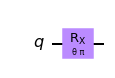
回転ゲート
2. 学習用量子回路
次に、古典機械学習のモデルに相当する学習用量子回路を準備します。古典機械学習で、さまざまなモデルが用いられるように、学習用量子回路は、さまざまなものが考えられます。学習用量子回路を構成する量子ゲートをパラメータ付きとし、そのパラメータが、古典機械学習における重みに相当します。古典機械学習では、活性化関数のもつ非線形性が重要な働きをしますが、量子機械学習では測定が、その働きをします。学習用量子回路の出力は、一般的には、測定結果の期待値です。
3. 損失関数
入力データ
4.回路パラメータ更新
古典量子ハイブリッドアルゴリズム VQEやQAOAと同様に、損失関数の計算と、
量子機械学習の実例
ここでは、Qiskit のテキストブック Qiskitを使った量子計算の学習 の中から、PyTorchとQiskitを用いた量子古典ハイブリッド・ニューラル・ネットワーク( https://qiskit.org/textbook/ja/ch-machine-learning/machine-learning-qiskit-pytorch.html)に掲載されているプログラムを見てみることにします。プログラムのコメントを日本語化し、プログラムの一部を用いています。
MNIST の手書き文字のなかから、0と1の数字を分類するという簡単なものです。ネットワークの構成は、次のの通りです。まず、MNISTの手書き文字を、二段階の二次元CNNとmax pooling を行い、フラット化し、2層のフルコネクト層をへて、サイズを1まで縮小します。最後のフルコネクト層の出力値が、パラメータ
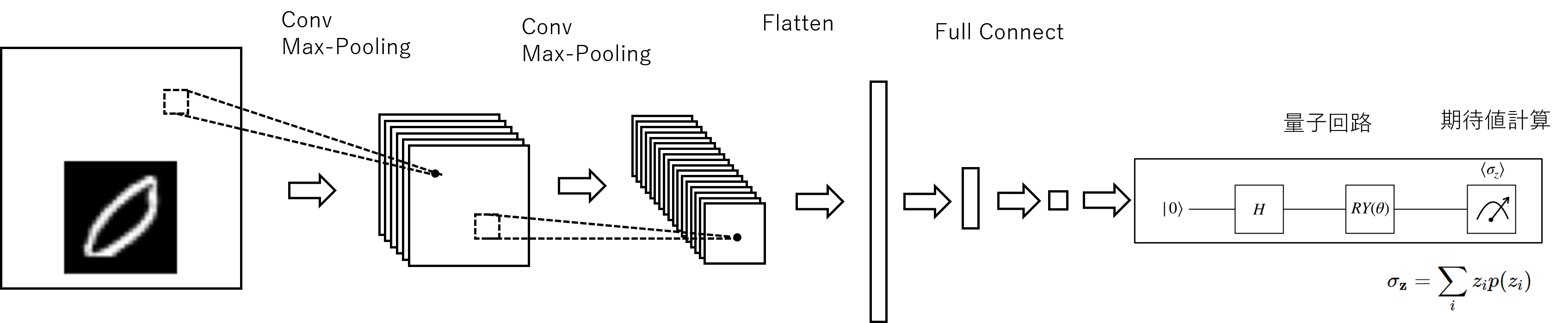
ネットワークの構成
パッケージのインポート
まず、必要なパッケージをインポートします。
xxxxxxxxxximport numpy as npimport matplotlib.pyplot as plt
import torchfrom torch.autograd import Functionfrom torchvision import datasets, transformsimport torch.optim as optimimport torch.nn as nnimport torch.nn.functional as F
import qiskitfrom qiskit.visualization import *Qiskitを用いた量子回路を作成します
ネットワーク構成の量子回路の部分です。
xxxxxxxxxxclass QuantumCircuit: def __init__(self, n_qubits, backend, shots): # --- 用いる量子回路を定義します --- self._circuit = qiskit.QuantumCircuit(n_qubits) #n_qubitsの量子回路を用います all_qubits = [i for i in range(n_qubits)] # all_qubitsを定義します self.theta = qiskit.circuit.Parameter('theta') # theraを定義します self._circuit.h(all_qubits) # すべのてqubitにアダマールゲートを追加します self._circuit.barrier() # barrierを追加します self._circuit.ry(self.theta, all_qubits) # すべてのqubitに、回転角θのRyゲートを追加します self._circuit.measure_all() # 測定します。 # ---------------------------
self.backend = backend self.shots = shots def run(self, thetas): # 量子回路の計算を実行します job = qiskit.execute(self._circuit,self.backend,shots = self.shots, parameter_binds = [{self.theta: theta} for theta in thetas]) result = job.result().get_counts(self._circuit) # 計算結果からカウント値を取得します counts = np.array(list(result.values())) # カウント値です states = np.array(list(result.keys())).astype(float) # 状態です # おのおのの状態にたいする確率を計算します probabilities = counts / self.shots # 期待値を計算します expectation = np.sum(states * probabilities) return np.array([expectation])barrierは、回路の一部を分離するためのもので、回路コンパイル時に最適化または書き換えをバリア間でのみに制限する設定です。
PyTorchを用いた量子古典回路の作成
PyTorchを使った逆誤差伝搬に必要な関数です。逆誤差伝搬は、損失関数の差分をとることによって、損失関数の 勾配を直接計算します。古典機械学習において、逆誤差伝搬に深く立ち入らないように、ここでも、プログラムの詳細には立ち入りません。上で作成した量子回路の順伝搬、逆伝搬を行うためのクラスであるということに留めます。
xxxxxxxxxxclass HybridFunction(Function): def forward(ctx, input, quantum_circuit, shift): """ 順伝搬計算 """ ctx.shift = shift ctx.quantum_circuit = quantum_circuit
expectation_z = ctx.quantum_circuit.run(input[0].tolist()) result = torch.tensor([expectation_z]) ctx.save_for_backward(input, result)
return result def backward(ctx, grad_output): """ 逆伝搬計算 """ input, expectation_z = ctx.saved_tensors input_list = np.array(input.tolist()) shift_right = input_list + np.ones(input_list.shape) * ctx.shift shift_left = input_list - np.ones(input_list.shape) * ctx.shift gradients = [] for i in range(len(input_list)): expectation_right = ctx.quantum_circuit.run(shift_right[i]) expectation_left = ctx.quantum_circuit.run(shift_left[i]) gradient = torch.tensor([expectation_right]) - torch.tensor([expectation_left]) gradients.append(gradient) gradients = np.array([gradients]).T return torch.tensor([gradients]).float() * grad_output.float(), None, None
class Hybrid(nn.Module): def __init__(self, backend, shots, shift): super(Hybrid, self).__init__() self.quantum_circuit = QuantumCircuit(1, backend, shots) self.shift = shift def forward(self, input): return HybridFunction.apply(input, self.quantum_circuit, self.shift)データの準備
まず、MNISTのデータから、0と1を含む画像を選択します。
学習データ
xxxxxxxxxx# 最初の100個のデータを用いますn_samples = 100
# 学習データを準備しますX_train = datasets.MNIST(root='./data', train=True, download=True, transform=transforms.Compose([transforms.ToTensor()]))
# 数字0と1だけを残します idx = np.append(np.where(X_train.targets == 0)[0][:n_samples], np.where(X_train.targets == 1)[0][:n_samples])# 学習データとラベルですX_train.data = X_train.data[idx]X_train.targets = X_train.targets[idx]
# データのローダですtrain_loader = torch.utils.data.DataLoader(X_train, batch_size=1, shuffle=True)学習データの表示
xxxxxxxxxxn_samples_show = 6 # 表示するサンプル数
data_iter = iter(train_loader)fig, axes = plt.subplots(nrows=1, ncols=n_samples_show, figsize=(10, 3))
# 6個のサンプルを表示しますwhile n_samples_show > 0: images, targets = data_iter.__next__()
axes[n_samples_show - 1].imshow(images[0].numpy().squeeze(), cmap='gray') axes[n_samples_show - 1].set_xticks([]) axes[n_samples_show - 1].set_yticks([]) axes[n_samples_show - 1].set_title("Labeled: {}".format(targets.item())) n_samples_show -= 1
テストデータ
xxxxxxxxxxn_samples = 50 # サンプル数を50に設定します
# テストデータをダウンロードしますX_test = datasets.MNIST(root='./data', train=False, download=True, transform=transforms.Compose([transforms.ToTensor()]))
idx = np.append(np.where(X_test.targets == 0)[0][:n_samples], np.where(X_test.targets == 1)[0][:n_samples])# テストデータを準備しますX_test.data = X_test.data[idx]X_test.targets = X_test.targets[idx]
test_loader = torch.utils.data.DataLoader(X_test, batch_size=1, shuffle=True)ハイブリッド・ニューラルネットワークの作成
ネットワーク構成に示したように、コンボリューションとマックスプーリングなどからなる古典ニューラルネットワークと、一つのパラメータをもった量子回路からなるハイブリッド・ニューラルネットワークを作成します。
xxxxxxxxxxclass Net(nn.Module): def __init__(self): super(Net, self).__init__() self.conv1 = nn.Conv2d(1, 6, kernel_size=5) # 二次元CNN self.conv2 = nn.Conv2d(6, 16, kernel_size=5) # 二次元CNN self.dropout = nn.Dropout2d() # ドロップアウト self.fc1 = nn.Linear(256, 64) # フルコネクト層 self.fc2 = nn.Linear(64, 1) # フルコネクト層 self.hybrid = Hybrid(qiskit.Aer.get_backend('qasm_simulator'), 100, np.pi / 2) # 量子回路層
def forward(self, x): x = F.relu(self.conv1(x)) # 活性化関数 relu x = F.max_pool2d(x, 2) # マックスプーリング x = F.relu(self.conv2(x)) # 活性化関数 relu x = F.max_pool2d(x, 2) # マックスプーリング x = self.dropout(x) # ドロップアウト x = x.view(1, -1) # サイズ調整をする x = F.relu(self.fc1(x)) # 活性化関数 relu x = self.fc2(x) # 最後は、活性化関数なし x = self.hybrid(x) # 量子回路層 return torch.cat((x, 1 - x), -1)ネットワークの学習
最適化法として Adam 学習率 0.001 負の対数尤度損失関数、エポック数20でネットワークを学習させます。
xxxxxxxxxxmodel = Net()optimizer = optim.Adam(model.parameters(), lr=0.001)loss_func = nn.NLLLoss()
epochs = 20 # エポック数loss_list = []
model.train()for epoch in range(epochs): total_loss = [] for batch_idx, (data, target) in enumerate(train_loader): optimizer.zero_grad() # 順伝搬 output = model(data) # 損失を計算 loss = loss_func(output, target) # 逆伝搬 loss.backward() # 係数を最適化 optimizer.step() # 損失を記録する total_loss.append(loss.item()) loss_list.append(sum(total_loss)/len(total_loss)) # 損失曲線を表示する print('Training [{:.0f}%]\tLoss: {:.4f}'.format( 100. * (epoch + 1) / epochs, loss_list[-1]))Training [5%] Loss: -0.7380 Training [10%] Loss: -0.9153 Training [15%] Loss: -0.9282 Training [20%] Loss: -0.9393 Training [25%] Loss: -0.9463 Training [30%] Loss: -0.9515 Training [35%] Loss: -0.9585 Training [40%] Loss: -0.9637 Training [45%] Loss: -0.9713 Training [50%] Loss: -0.9657 Training [55%] Loss: -0.9710 Training [60%] Loss: -0.9758 Training [65%] Loss: -0.9765 Training [70%] Loss: -0.9804 Training [75%] Loss: -0.9873 Training [80%] Loss: -0.9887 Training [85%] Loss: -0.9894 Training [90%] Loss: -0.9873 Training [95%] Loss: -0.9904 Training [100%] Loss: -0.9870
学習曲線を表示します
xxxxxxxxxxplt.plot(loss_list)plt.title('Hybrid NN Training Convergence')plt.xlabel('Training Iterations')plt.ylabel('Neg Log Likelihood Loss')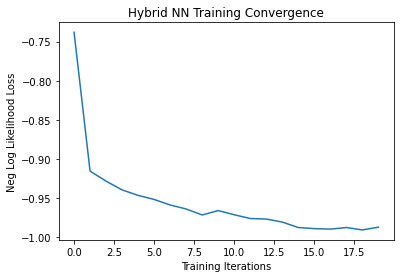
テストを行います。
xxxxxxxxxxmodel.eval()with torch.no_grad(): # テストデータで推論し、損失と精度を調べます correct = 0 for batch_idx, (data, target) in enumerate(test_loader): output = model(data) pred = output.argmax(dim=1, keepdim=True) correct += pred.eq(target.view_as(pred)).sum().item() loss = loss_func(output, target) total_loss.append(loss.item()) print('Performance on test data:\n\tLoss: {:.4f}\n\tAccuracy: {:.1f}%'.format( sum(total_loss) / len(total_loss), correct / len(test_loader) * 100) )Performance on test data: Loss: -0.9847 Accuracy: 100.0%
損失は、-0.9837、精度は、100%です。
推論結果を表示します
xxxxxxxxxxn_samples_show = 6 # 表示するサンプル数count = 0fig, axes = plt.subplots(nrows=1, ncols=n_samples_show, figsize=(10, 3))
# 推論結果を表示しますmodel.eval()with torch.no_grad(): for batch_idx, (data, target) in enumerate(test_loader): if count == n_samples_show: break output = model(data) pred = output.argmax(dim=1, keepdim=True)
axes[count].imshow(data[0].numpy().squeeze(), cmap='gray')
axes[count].set_xticks([]) axes[count].set_yticks([]) axes[count].set_title('Predicted {}'.format(pred.item())) count += 1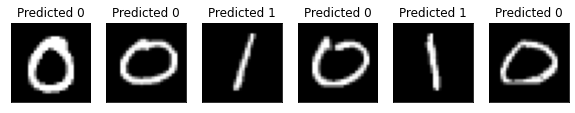
ただしく推論ができています。
このプログラムは、あくまで量子機械学習の概念を示すために作成されています。このネットワークは、量子層がなくても、ちゃんと学習されます。また、量子回路も、エンタングルメントを含まないものです。量子機械学習を有効なものにするには、さらなる改善が必要です。
サンプルプログラムについて
サンプルプログラムは 、 Apache 2.0ライセンス で配布されているプログラムが含まれています。各サンプルプログラムには、出典を明記するとともに、変更を加えた場合は、変更点を記載しています。
参考文献
(1)IBM Quantumで学ぶ量子コンピュータ 湊雄一郎他著
(2)インターフェース 2019年3月号
(3)Qiskit 0.32.0 documentation (Japanese)
(6)ibm-quantum-challenge-fall-2021
(8)Qmedia
(9)量子コンピューターの基礎 藤井 啓祐 オペレーションズ・リサーチ 2018 年 6 月号
(10)量子コンピュータの応用 - QAOAの仕組みとこれを応用した組合せ最適化問題のプログラミング
(11)Solving combinatorial optimization problems using QAOA
(12)QC — How to build a Quantum Computer with Superconducting Circuit?
(13)IBM Research Blog What’s in a qubit?
(14)P. J. J. O’Malley et al., Scalable Quantum Simulation of Molecular Energies, PHYSICAL REVIEW X 6, 031007 (2016)
Copyright © AiSpirits All Rights Reserved.